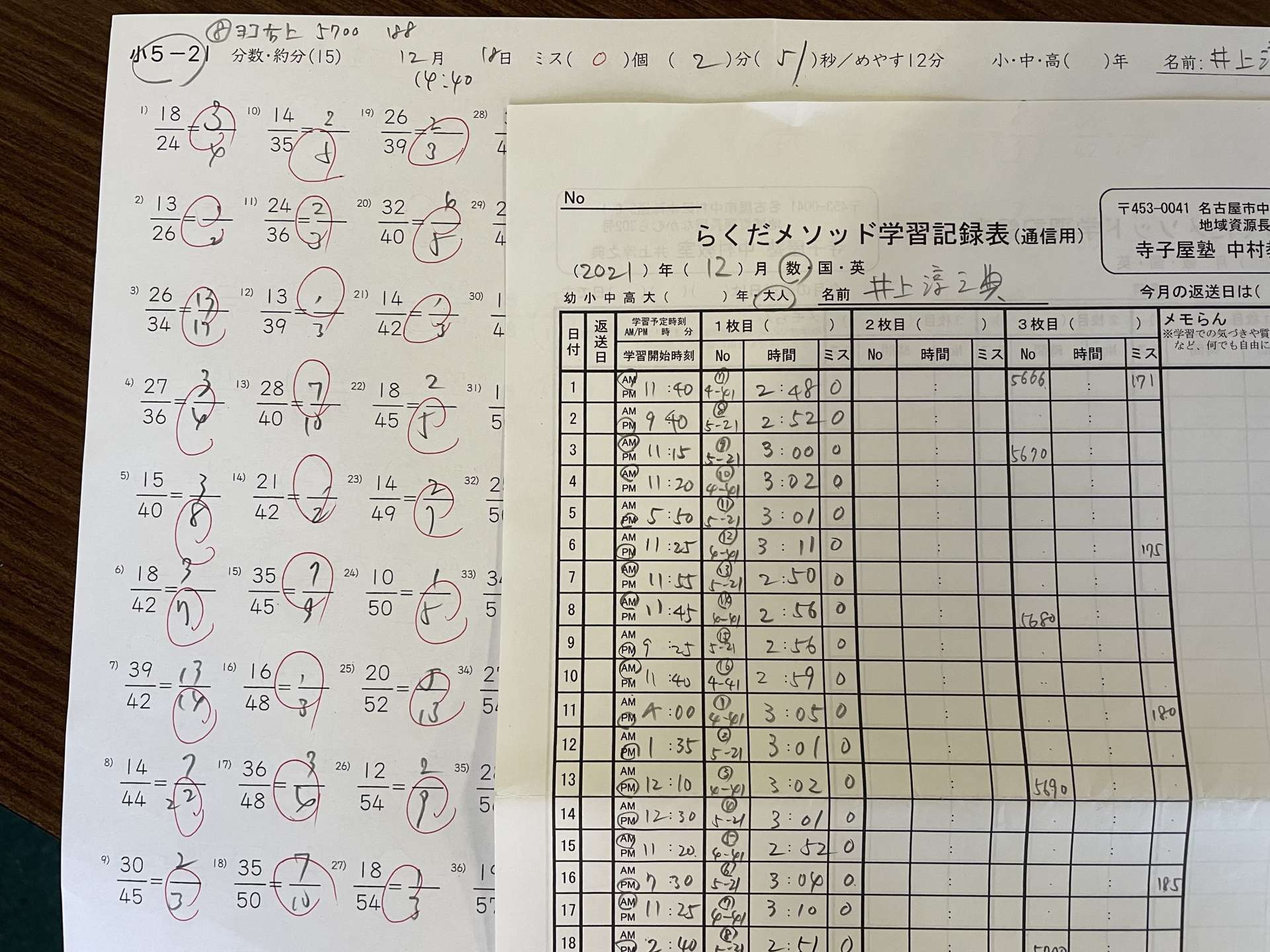
分数約分プリント５７００枚に

12/7に書いたこちらの記事のとおり、いまわたしは、分数の約分問題が９９問並んだ小４−４１と小５−２１を１枚ずつ計２枚、毎日欠かさずにやると決めて取り組んでいて、本日12/18で通算５７００枚目となりました。

 

合格したら次のプリントに進むというのが、このメソッドの基本ルールではあるんですが、目的次第でルール以外のやり方はあり得るし、どのプリントをやってもそれなりに学べることがあるというのが現在の実感です。

 

同じプリントを繰り返し繰り返しやっているので、いまではほとんどの問題に対して、見た瞬間に答がおもい浮かぶようになっています。よく「これだけやっていると答を憶えてしまいませんか？」と聞かれるんですが、そうやって問われることの前提に、「機械的に答を憶えてしまうことは良くないコト」という見方が隠れているように感じることが多々ありました。

 

でも、答を憶えることはけっして悪いことではありません。たとえば、誰もが小学２年生で習うかけざんの九九は、理屈抜きに丸暗記するしかないプログラムの代表選手ですし、百人一首だって憶えていなければカルタは取れませんから。

 

ただ、これだけたくさんの枚数を繰り返してやってきたからこそ気づいたことでもあるんですが、この約分問題の場合においては、過去にやったことで脳に記憶された答を引き出してくるスピードよりも、実は、自分の視覚に入って来た目の前のプリントの問題をその場で解くスピードのほうが早いんです。

 

どうして問題をその場で解いた方が早いかというと、たとえば、自分の目の前に大きな蛇がいることに気づいたとしましょう。そんなときは、蛇を見た瞬間に身体から反射的に逃げるのであって、「この蛇は自分を咬むかもしれない」と過去の記憶を引き出してきて頭が判断してから逃げるという行動に移るのではないですよね？　そんなこと考えてたら、逃げ遅れて咬まれてしまいますから。

 

わたしたち人間は、脳が判断した結果として身体を動かしているようにおもうかもしれませんが、それは錯覚であって、実は脳がすべての行動をコントロールしているわけではないんですね。このスタイルでのプリント学習を続けてきて、これが実感できたことは結構大きかったです。

 

あと、今では1枚やるのにだいたい1分半でできるので、２枚合わせて３分前後になるんですが、ちょっと気を緩めすぎたり、力が入りすぎたりするとすぐに３分を超えてしまいます。よって、３分以内でできているかどうかが、自分の今のコンディションを知るのに格好のわかりやすいバロメーターになっています。

 

問題を解くのに３分、答え合わせに２分、記録とふりかえりで１〜２分と全部で６〜７分あればできることなので、誰にも平等に２４時間与えられている１日の中で、これができない理由はありません。でも、人間の大脳は、行動にブレーキをかけることが得意なんですね。

 

皆さんも多分経験があるとおもうんですが、そういう脳の特質を知らずにいると、「自分が～しなかったのは、～だからだ」と、まったく別の次元にある２つの事柄を、因果関係で結びつけてしまうだけでなく、自分の行動の言い訳を考えてしまうわけで、どんなにうまい言い訳を考えたところで、それだけではできるようになっていかないのに、その巧妙さはほとんど天才的と言ってもいいかもしれません。笑

たとえば、やろうとしたことができなかったときに、仕事が忙しいからとか、疲れてやる気がしなかったからとか、すぐに言い訳はおもいつきますよね。仕事が忙しいかどうかとか疲れたかどうかということに客観的指標があるわけではなく、いずれも多分に自分の感覚的かつ主観的判断でしかなく、だいたい自分の勝手な都合でしかないんですが。

 

そうした外的な環境や状況に対する自分の認識と、自分がやろうとしたことをするかしないかという、２つの事柄を安易に結びつけることなく、別次元のことだと切り離して考えられるかどうかが、事実を土台に物事を把握しようとする姿勢づくりや、大脳思考に縛られず、気分に振り回されずに行動しようとするときには、大事なポイントとなるということも、だんだんとわかってきました。

 

冒頭書いたとおり、いまのわたしは「どんなことがあってもこのプリントはやる」と決めていて、２０１４年からこのスタイルで学習しているのでもう８年目になるんですが、それでも元旦から大晦日まで、１年通して続けられた年が１回もありません。ちなみに今年は、３月４月５月にできなかった日が１日ずつあり、また６月には３日できなかったので、合計で６枚できなかったことになります。

 

３月以降はそれ以前と比較すると、わたしの食生活がガラッと変わってしまうという大変動があったので、もしかするとそうした大変動の影響だったかもしれないのですが、前に書いた通り因果関係で結びつけたところでできるようにはなりませんし、ほんとうのところはわかりません。

 

たかが算数プリント、されど算数プリント・・・その処し方、向き合い方次第で、少し大げさに聞こえるかもしれませんが、それまで見えていなかった未知の世界が見えてくることもあるわけです。

 

たとえばわたしの場合、何かひとつのことに集中すると，それ以外のことがすっ飛んでしまい、同時並行的に意識を分散させることがなかなかできない自分や、イレギュラーなことに弱い自分、根強い後回し癖がある自分の姿がこのプリント学習のお陰で見えてきました。

 

自分でちゃんと決めていなければ、できない自覚は生まれません。何をどのようにやるかが他から一切強制されず、続けてやると自分で決めているからこそ、できない壁に突き当たったときに、今まで見えなかった自分が見え、気がつかなかった自分に気がつくようになって、より自覚的な見方ができるようになってくるわけです。

 

５７００枚やってもこの学習の面白さや価値がすべてくみ取れたとは言い切れないところがあり、まだまだしばらく探究は続きそうです。