闇雲に数こなせばいいってわけじゃない!(その2)
2022/10/16
いつも日曜は、古典研究カテゴリーの記事を
投稿しているんですが、今日はイレギュラーで
昨日書いたらくだメソッドについての記事の続きです。
記事の最後で、山口周さんと楠木建さんの対談本
『「仕事ができる」とはどういうことか』から、
島田紳助さんが若手の芸人たちに向かって言っていた
「努力するな」という話を引用して紹介しました。
お笑い芸人として一流になりたければ、
ひたすら漫才の稽古をし続けるというような
不毛な努力ではなく、その上位のレイヤーにある
「どうしたら売れるか」という
お笑い芸人としての戦略をちゃんと考えるという
努力をしないとダメだよってことでしたね。
つまり、引用した本のタイトル
『「仕事ができる」とはどういうことか』を
もじって言うなら、
『「勉強ができる」とはどういうことか』を
ちゃんと考えて臨もうということになりますか。
昨日にも書いた通り、小学校4年生で習う
2桁のわり算は、一説では、半数以上の子どもたちが
ここで躓いてできなくなるとさえ言われている
難関単元なのです。
ですから、ただ闇雲に数をこなすやり方でなく
どうやったらこの単元が克服できるかという
明確な戦略を持って臨む必要があるんだと。
こちらのインタビュー記事で詳しく話したんですが、
らくだメソッドは、平井雷太さんが、
ご長男の有太くんという
生身の人間を相手に開発された教材です。
つまり、何かを教えるという場合において
最も難しい間柄とされる
親子という関係の中で生まれたものですから、
どうやればこの単元が確実にできるようになるか
という戦略については、
細部まで徹底して考え抜かれています。
では、具体的にどのように
らくだメソッドがつくられているか
順を追って書いて行きましょう。
たとえば、124÷17という割り算を考えてみます。
72÷8であれば、
8 × □=72 の□を求める計算として
72の中に8がいくつ入っているかを考えるのは
九九の逆算をすればすぐに出ますが、
124÷17だと
124のなかに17がいくつ入っているかが
九九のようにはすぐにはわかりません。
つまり、この場合、適当に当てずっぽうで
「17 × ある数」のかけ算をやってみて、
124に限りなく近い数を見つけるようなやり方では、
そのたびごとに何度も
「17 × ある数」のかけ算をしなくてはならず、
その面倒なことといったらありません。
そこで、らくだメソッドでは
「2けたのわり算」単元の最初のプリント
小4−6では冒頭4問が導入に宛てられているんですが、
こんな具合にはじまります。
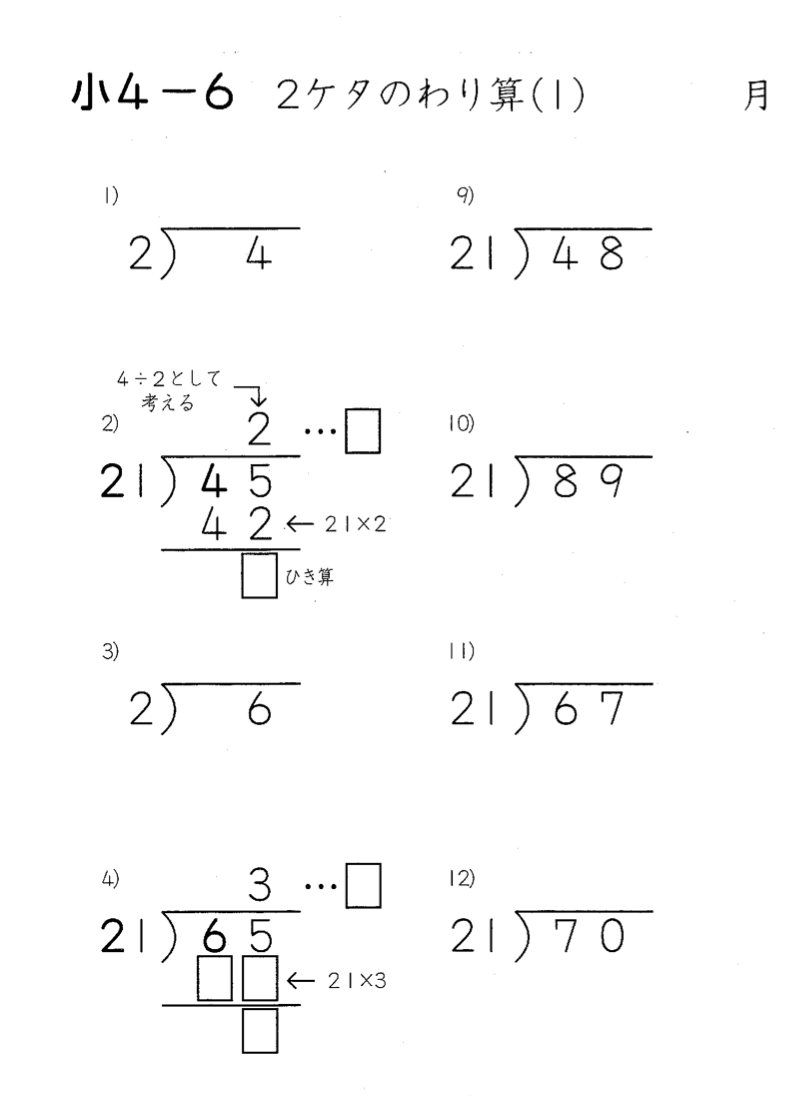
2番の問題では、わる数もわられる数も両方とも、
まず、一の位を隠して
太字数字だけでわり算4÷2をやって
仮の商を立てていますが、
一の位を四捨五入するのではなく、
切り捨ててしまえばいい。
つまり、2番の問題 45 ÷ 21 は、
1番の問題のような
一けたのわり算 4÷2 ができる人なら
できてしまうというわけです。
4番の問題 65÷21 であれば、
6÷2でやってみるといった具合ですし、
9番から12番の問題も同じやり方で
解けることがお判り頂けるでしょう。
しかし、このやり方でやっていくと、
次の問題のように、一の位を隠してわり算をやっても、
そのままの数では答にならない場合が出てきます。
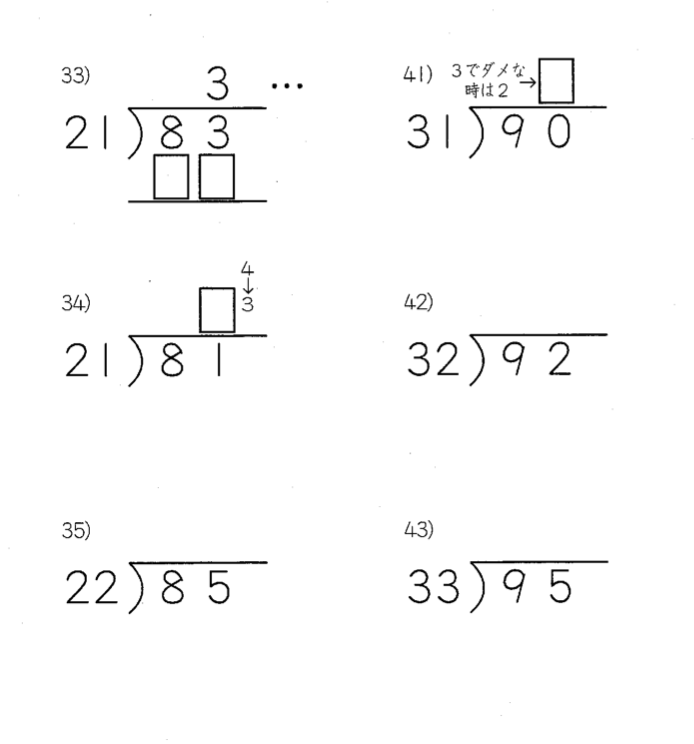
この問題は小4−7のプリントの途中部分なんですが、
33番の 83÷21のように、
8÷2=4の答を出すと、21×4=84となって、
そのままの数では答になりません。
つまり、わられる数83より大きくなってしまい、
33番の答は4ではわれないことを知らせるため、
最初から答のところには、3と入れてあります。
その次の34番の問題では
答の右わきに小さい数字で「4→3」と記入し、
立てた答から1つ下げる場合があることを
事前に示しています。
小4−6と小4−7は、2けた÷2けたですが、
小4−8のプリントからは、3けた÷2けたになります。

1番から49番まではわる数もわられる数も両方とも、
一の位を隠すこれまでのやり方を
そのままやれば答が出せる問題ばかりが並んでいます。
たとえば、上の画像にある1番の問題は、
一の位を隠して
107÷21 は 10÷2 として考えればいいので。
![]()
ところが、上の画像にある50番からは違います。
49番は11なので2でわって5が答になりますが、
50番は12÷2でも6ではわれませんから、
小4−7のプリントで学習した
1つ減らさなければならない問題の応用で、
22×5が110になることは、
前の問題49番を見れば分かるようになっています。
つまり、51番と52番の関係は、
49番と50番の関係と同じようになっていますし、
56番の問題まではすべてわる数が22になっていて、
一の位を隠してわり算をすればいい問題と
そのまま答えにならない問題が混ざっています。
また、57番から64番までの問題は
すべてわる数は23なんですが、
すべて一の位を隠してわり算をして立てた答から
1つ減らせば答になる問題が続いています。
だいぶ長くなってしまったので、続きはまた明日に!




