闇雲に数こなせばいいってわけじゃない!(その3)
2022/10/17
昨日書いた記事の続きです。
昨日の記事では、
らくだメソッド小4-6から小4-8のプリントに
2けたのわり算ができるようになるために
どんな工夫がされているかを具体的に書きました。
それで、一昨日、昨日の記事に
闇雲に問題をたくさん解けばいいんじゃなくて、
「勉強ができるとはどういうことか」
「2けたのわり算は
どうすれば確実にできるか」という
明確な戦略を立てて臨む姿勢が大切と
書いたこともあり、
小4-8より先のプリントの説明に進む前に、
現実に、いま小学4年生の子どもで、
2けたのわり算ができなくて困っている場合に
らくだメソッドであれば
具体的にどんな提案ができるかという話も、
ちゃんとした戦略をもって臨むということの
確認の意味でここに書いておこうとおもいます。
たとえば、こちらのページ(教えてgoo)に
次のような相談が寄せられていました。
(引用ここから)
ーーーーーーーーーーーーーーーーーー
現在小4の妹なんですが、
算数が大の苦手で、わり算が根本からわからず、
宿題もなにも出来ないという状態です。
今さっきも、母親が宿題を教えようにも、
いくら説明しても妹はわからないと言って、
親はやる気が無いんだと
教えるのをやめてしまいました。
それで、泣き喚いて怒って終わり。
いつもこの調子で、1年生のころから足し算は
指を使って数えているし、九九もあやしいです。
できるといいはっていますが、
聞いてみると間違っています。
算数の教え方の本を読んだりして、研究していますが、
そもそも本人は勉強をやるのが大嫌いで、
一緒に復習しようとこちらが言っても
見向きもしません。
自分含め、上2人は普通以上の学力はあります。
学校以外の教材は●●ゼミのがありますが、
結局まだ習っていないとか、わからないとか言って、
入ったりやめたりを繰り返してきました。
塾に通わせるなど他人に丸投げしようにも、
学習意欲が無いのですぐにやめてしまうと思います。
友達はそこそこいるので、
学校は楽しく通えていますが、
授業中どんな態度かはわかりません。憶測ですが、
授業の内容はさっぱりわからないと思うので、
ひたすら板書をしているのかもしれません。
どうしたら算数が出来るようになるでしょうか。
ーーーーーーーーーーーーーーーーーー
(引用ここまで)
あるある話ですね〜
ベストアンサーを含め10名から回答が寄せられ、
その各々の賛否はともかく、
それぞれに異なった観点でレスポンスしているので、
興味ある方は、リンク先の記事を
ご覧になってみてください。
ただ、お姉さんが書かれたこの文面を読むだけでは、
算数ができない具体的な原因が
わたしにはいまひとつわかりませんでした。
よって、もしわたしがこのご相談を受けたのであれば、
どうして算数の勉強が嫌いになってしまったかなど
もうすこしインタビューを重ねて、
背景などを探ってからアプローチするでしょう。
仮にこのような相談が寄せられた場合に、
らくだメソッドであればどのように対応するかを
すこし書いておこうとおもいます。
わり算は小学3年生の算数で習い始めるんですが、
わり算という演算は、
たし算、ひき算、かけ算を全部使っているんですね。
たとえば、次のような問題です。
|
【問題】 34人の子どもが5人がけのイスに座るとき イスは全部で何きゃく必要ですか?
〔式〕34÷5=6あまり4 または 34−(5×6)=4
あまった4人が座るために もうあと1きゃく必要ですから 6+1=7
〔答〕7きゃく
|
つまり、4年生の2けたのわり算ができない場合、
その原因は一律でなく、人によって違うんですが、
でも、わり算だけができない場合はほとんどなく
前に習ったたし算、ひき算、かけ算のいずれかが、
(あるいはそのすべてについて)
習熟していないケースが大半でしょう。
ちなみに、四則演算相互のつながりについては、
次の記事に詳しく書きましたので、
関心ある方はご覧ください。
それで、らくだメソッドでは、
易しい問題から難しい問題へと進んで行く
スモールステップの形をとり、
1枚1枚のプリントに「時間」「ミスの数」の2軸で
合否のめやすが設けられていますから、
単元のまとめになっているプリントをただやるだけで、
どこでつまずいているかが一目瞭然になるのです。
(寺子屋塾の体験学習でお渡ししている
お試しプリント7種類はこの観点で選んでいます)
このテーマについても次の記事に詳しく書いたので、
ここまで読まれてあまりピンと来ない方は
ご覧になってみてください。
さて、お待たせしました!プリントの説明に戻ります。
小4−9の冒頭は次のようになっていますが、
この辺りは1枚前の小4-8の問題と同じレベルです。

つまり、上の1番の問題は、
10÷3=3あまり1なので商3を立て
3でわれるのでOKなんですが、
2番の問題は12÷3=4 と4を立てても
2×4=8 の8が引けませんから、
4ではわれず、
4から1減らして「3あまり24」が答です。
小4-9のプリントは、34番の問題まではこのように
そのまま一の位を隠してわり算すればできる問題と
そのわり算の答を仮の商として、
そこから1減らしてできる問題のいずれかです。
ところが、次の画像のように、
35番からは仮の商から1減らすだけでは
できない問題が混ざってきます。
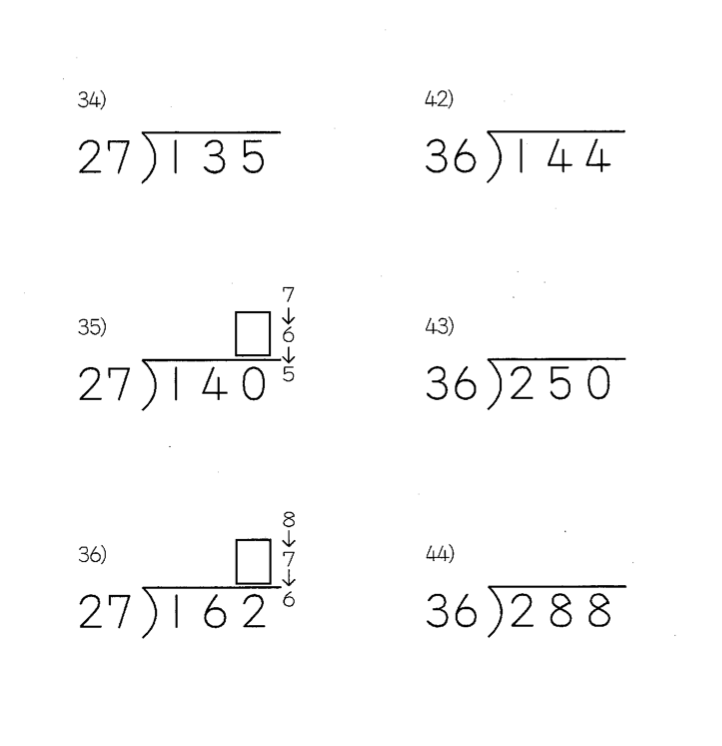
上の画像のように、35番の140÷27は、
14÷2=7ですが、7→6→5という風に、
仮の商から2つ減らさないと答が出ませんし、
続く36番の162÷27も同じく2つ減らさないと
正しい答を出せない問題になっています。
小4-9から小4-13までのプリントは、
ひとつひとつの問題のグレードは変わらないのですが、
プリント1枚の中にある全64問を見ると
|
①一の位を隠してわり算するだけでできる問題 ②仮の商から1減らしてできる問題 ③仮の商から2つ減らさないと答が出ない問題 |
の①から③までが混在し、
プリント番号が進むほど②と③が多くなっていて
だんだん難しくなっていくように構成されています。
続く小4−14のプリントには、
次の画像の21番の問題のように
わる数の十の位の数字が小さいため、
一の位を隠して計算すると22÷2=11となり
11→10→9→8 というように
3減らさないと答が出ない問題が含まれてきます。

いずれにしても、このように
わる数とわられる数の一の位を隠しながら、
どんな数を立てれば答になるかというやり方で
計算をしていくと、3けた÷2けたの問題では、
次のような問題が最も難度が高いことになります。
![]()
上記64番の問題171÷19は、
3けた÷2けたのプリントのうちで
いちばん難しい小4-15の最後の問題です。
でも、前提として小4-15までのプリントは、
わり算の商がすべて1けたになる問題なので、
商が11や10になるはずがありませんから、
仮の商を9から順番に立てていって、
それで割れなければ
1ずつ減らしていけばいいと指導しているので、
その通りにやれれば、
実際にはこの問題を解くのに
それほど苦労することはありません。
つまり、3けた÷2けたの問題は、
一の位を隠しながらわり算をして、仮の商を立て
それで割れないときには仮の商から
1つ減らす → 2つ減らす → 3つ減らす・・・
という流れが、そのまま易から難への
グレードになっていると言ってよいでしょう。
さて、このように、
らくだメソッド「2けたのわり算」のプリントは
小4-6から小4-15まで計10枚で構成され、
各プリントとも全64問を
12分台でできれば合格としているんですが、
これは、
問題を見た瞬間、商に何が立つかが分かる習熟度
を意味しています。
つまり、この小4で習う「2けたのわり算」単元は、
ただ単に問題の解き方を知っているだけでは
太刀打ちができない課題を含んでいるわけですね。
「わかる」と「できる」は違うのですから。
よって、この課題をクリアするための戦略として、
「仮の商を立てる → 引けない → 減らす」という
正しい手順を守るだけでなく、
問題を解くめやす時間とミスの数という
制約を課しつつ、
正しい商にたどり着くまで
トライアンドエラーを繰り返しながら
見通しを立てる練習や、
いちいち頭で考えなくても
自然にそれができてしまうような数感覚の養成が
必要となってくるわけです。
この続きはまた明日に!




