自分の器を拡げるためにできること（その５）

一昨日の記事の続きです。

 

Facebookに庭の写真をアップして

天気と予定についての記事を投稿し始めたのは、

2011年11月のことでした。

 

それが毎日無理なく

投稿し続けられるようになるまでに

結局1年以上かかったということ、

またそれは、世間話が苦手だった当時の自分が

天気についての情報を仕入れるためだった

というのが当初の目的だったこと、

そして、その投稿をずっとし続けてきたことで、

当初目的としていた成果以外にも

さまざまな副産物が得られたことなど、

これまで書いてきた通りです。

 

毎日し続けるという課題が

クリアできるようになったので、

また別の課題にチャレンジしてみようとおもったのは

2013年春のこと。

 

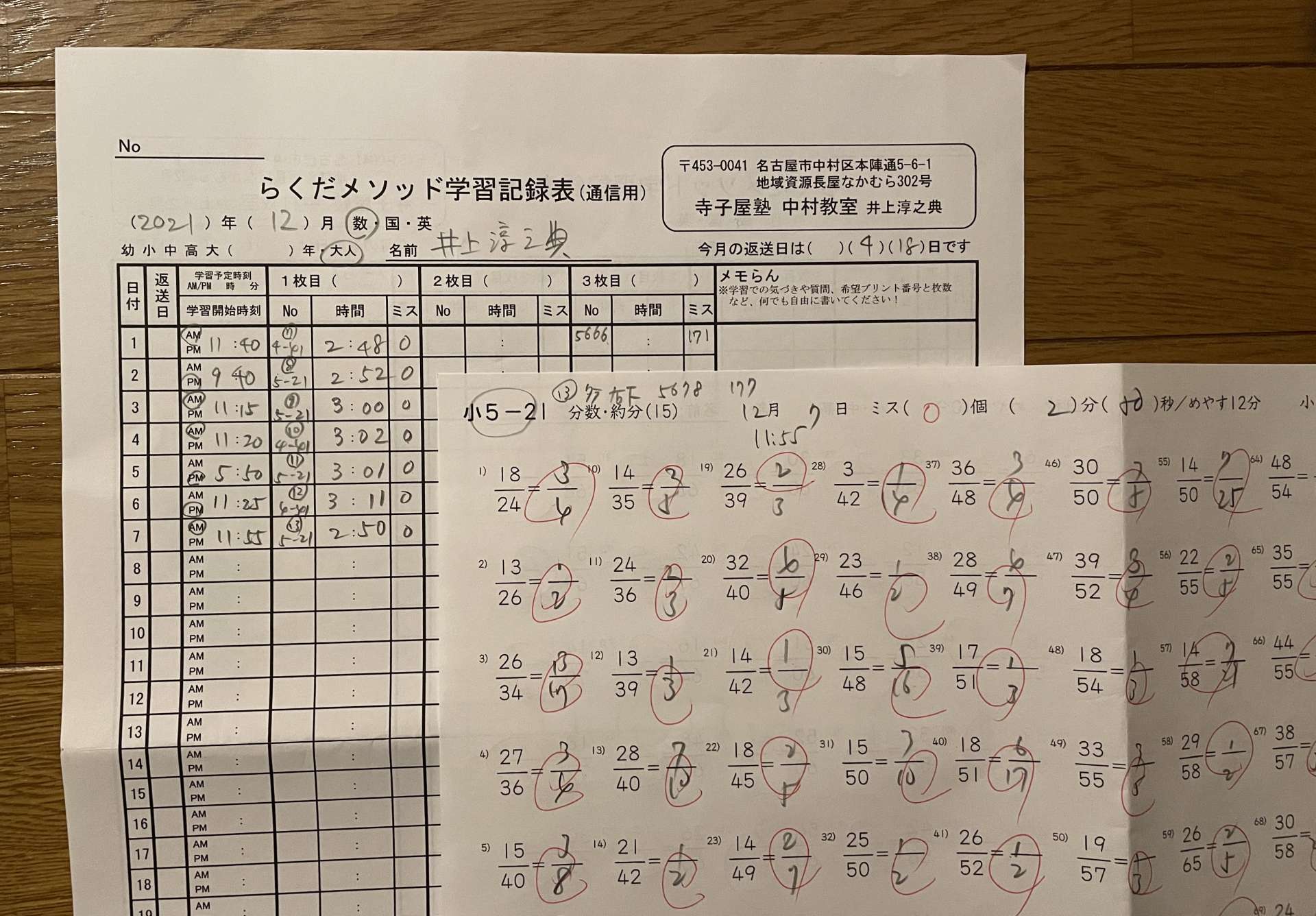
小学４年生で習う分数の約分問題が99題並んでいる

小４−４１のプリントをやり始めたのは、

2013年5月13日のことでした。

 

現在は、小４−４１と全く同じスタイルで

分数の約分問題が９９題並んでいる

小５−２１のプリントと小４−４１の計2枚を

1日にやっていているんですが、

2013年5月13日を起算として合計枚数は

本日分で５６７８枚めとなりました。

 

最初は同じプリントを180枚やる目的で始めたんですが、

そのときには分数の約分プリントを

５０００枚以上もやり続けることになろうとは

想像だにしませんでした。

 

2013年の１年間で

当初の目標だった180枚を学習し終え、

2014年の年明けに書いた

ふりかえりの文章があり、

2017年秋にblogで公開したことがあったのですが、

読まれていない方も

少なくないとおもいますので、

以下にそれを再録することにしました。
 

このふりかえり文を書いて以後の気づきもまた
興味深いものがいろいろあり、

それこそ本が1冊書けてしまうんじゃないかと

おもえるほどの分量があります。

 

寺子屋塾を始める前に、
「ひとつのことを10年間、毎日やり続けたら、

　そのことで人生が語れるようになる」と

言って下さった方があったんですが、
いまのわたしは、
だいぶその領域に近づいている実感がありますし、
やり始める前の自分には

まったく想像できなかった世界が訪れていて、

いつかはそれをすべて総括して

書いてみたいとおもっています。

　

ーーーーーーーーーーーーーーーーー

らくだメソッド・算数小４－４１（分数約分のまとめ）
　2013.5.13～2013.12.28　ふりかえり　

 

【この学習をはじめたきっかけ】
2014年は、わたしがらくだメソッドを使った

教室〝寺子屋塾〟を始めて20周年を迎えます。

このメソッドは、常に学習者の

〝今〟を浮き彫りにするため、

マニュアル的対応はほとんど通用しません。

 

そのため、指導マニュアルのようなものが

一切用意されていないのですが、

この20年の間にたくさんの生徒と接するなかで、

わたし自身も数え切れないほど

多くのことを学んできました。

 

またその一方で、指導経験をつめば積むほど、

その経験が却って邪魔をして、

わかったつもりになってしまっているのではないか、

ということも気になっていました。

 

以前は、指導者対象の研修会が

比較的頻繁に持たれていたのですが、

最近はそういう機会もほとんどなく、

今一度わたし自身原点に戻って

学び直したいとおもったことが一番大きな動機です。

 

つまり、このメソッドで学ぶことが、

今のわたし自身にとっても新たな気づき、

変化、成長等を本当にもたらすのかどうか、

20年を１つの節目として

検証してみたいという想いがありました。

 

ただ、わたし自身は指導者ですから、

このメソッドの学習は過去にひと通り終えています。

 

それで、既に体験したやり方と

同じやり方で学習するよりは、

今までやったことのない新たなチャレンジを

した方が良いと思ったのですが、

そのためにどんな設定や枠組みが

適切なのかと考えたとき、

ふと浮かんだ言葉が

「180枚同じプリントをやり続ける」でした。

 

らくだメソッドの説明をするときに、

「何をどのように学ぶかについて、

　学習者が自分で決められる学習であり、

　自分でカリキュラムをつくれるメソッドである」

ということをお伝えしています。

 

そして、そのことの大事さを説明する際、

よくご紹介しているエピソードの１つに、

同じプリントを180枚やり続けた

小学生の生徒さんの話があります。

 

それは、そのプリントを学習すると

自分で決めたからこそできたのであって、

もし人から強制される状況下であったなら、

絶対にできないんだと。

 

でも、それは、わたしの教室で学んだ生徒の話でなく、

他の教室の指導者から伝え聞いた、

他の教室の生徒の話なのです。

 

わたし自身もらくだメソッドの学習は

「めやす時間内、ミス３個以内」であれば

次のプリントに進んでOKというルールに従って

学習したので、同じプリントを

180枚やりつづけたという経験はなく、

自分自身で実感していない単なる

受け売り情報を語っているにすぎません。

 

そこで、「もし今のわたしが同じプリントを

180枚やり続けたとしたら、

いったいどういうことが起きるだろうか？」

と自分に対しての興味が沸いたのです。

 

【5/13の時点で決めたこと】
・１日１枚だけ。２枚以上はやらない
・毎日やり続けることだけにとらわれない
　→毎日やれなかった時は、毎日やり続けたときと、

　　間が空いたときとでどう違うのか、

　　その間も２日空いたとき、３日空いたときとで

　　どう違うかを知るチャンスと考える
・いろんな時間帯、いろんな環境で

　やってみることを大事にして、やり方を固定化しない
・180枚続けることをとりあえずの目標にする

【なぜ小４－４１のプリントを選んだか】
ファシリテーションで

最も難しいと言われているスキルのひとつに、

合意形成の促進があります。

たとえば、AさんとBさんが

意見の食い違いで対立しているとき、

ファシリテーターがAさんの意見とBさんの意見に

共通する要素を瞬時に見つけて

その場で両者が納得するような提案ができれば、

合意形成が進むように思うのですが、

現実にはなかなか簡単ではありません。

 

らくだメソッドの小４－４１は、

分数の約分単元のまとめのプリントで、

問題が９９題並んでいます。

 

分数の約分問題を解くときの要所は、

分子と分母の異なる２つの数字を見て、

共通する最大の約数（因数）を

見つけられるかどうかにかかっています。

 

たとえば、38/95という分数を約分するときに、

38と95の最大公約数を探るわけですが、

共通因数19というのは素数ということもあり、

なかなかすぐにはおもい浮かびません。

 

あくまでわたしの勝手なアナロジーであり、

仮説ではあるのですが、この19が瞬時に閃いて、

38÷19＝2、95÷19=5　

　→　2/5　という計算ができるようになることを

異なる中に共通する要素を見つけられる能力の開発や、

合意形成のファシリテーションスキルの向上にも

つなげられないだろうか、ということです。

 

【学習プロセスで気づいたこと】
１枚のプリントをやり終えた時点で気づいたことは、

すぐに学習記録表などに書きとめるようにして、

１ヶ月に１回ぐらいの割で、

それまでの学習をふりかえって総括するよう心がけ、

時折facebookにもその内容を投稿していました。

以下はその要点です。

 

①早めに学習することで時間に対し自覚的になっていく

　学習する時間帯が遅くなるほど

　時間が長くかかり、ミスも増える
　→「プリントやらないと・・・」という思いを

　　ひきずりながら夜まで1日過ごすより、

　　早めに終わらせる方がメンタル的にスッキリする
　→算数の問題を解くことはアタマの準備体操にもなり
　　なるべく早い時間帯に終わらせたほうが良い
　→１日のうちのなるべく早めの時間に学習すると

　　決めていることによって、

　　時間に対する感覚が自覚的になっていくので、

　　周りの環境や出来事に流されがちな生活リズムを

　　自分でコントロールしやすい環境が生まれる。

 

②勉強は時間の長さよりも密度が大事

　たとえ１日５分の学習でも、続けることで

　学習した時間の総和以上の効果が生まれてくる。

　たとえば、５０分の学習を１日でやるよりも、

　５分の学習を10日休まず続けた方が

　同じ時間を使っていても効果が高い。
　→勉強はかけた時間ではなく、

　　中味と自分の姿勢、その質が問題。
　
③時間の計測は時間を気にせずに学習するため

　→早くやろうと時間を意識すればするほど

　　結果として時間は長くかかってしまう。
　→スピードアップを目的にせず、意識せず、

　　淡々とやることがスピードアップの秘訣
　→「学力向上は、

　　学びの結果として現れてきたものであって

　　目的ではない。学力向上の最大の秘訣は

　　学力向上を目的としないことにある。」（佐藤学）

 

④新記録が出る前は不調（スランプ）が続く
　→記録は少しずつ短くなるのでなく、

　　行ったり来たりしながらのプロセスを経て、

　　ある日、突然のように新記録が出ることが多い
　→「夜の終わりに朝が来る。しかし

　　　夜明け直前の闇は最も暗い」（むのたけじ）

 

⑤間違える問題はいつもだいたい同じ
　同じプリントを繰り返しやっているのに

　同じ問題で間違える傾向がある

　→どの問題で間違えやすいかを分析することで、

　　自分の思考パターンや癖がよくわかる
　→人はだいたいいつも同じ問題で躓いている

 

⑥気を緩めるとすぐ結果として現れる
　100枚を超えるあたりから、

　ミスがほとんどなくなってきたのですが、

　それでもたまに１つ２つ間違えることがあり、

　思わぬ処に伏兵が隠れていたという感じがした。

　150枚を超えたあたりになってようやく

　百発百中状態に近づいたが、それでも

　時間を急ぐとミスをする。
　→油断大敵！伏兵に注意！

 

⑦場所や筆記具、身につけるものの影響の大きさ
　これらの影響は、

「めやす時間内、ミス３つ以内であれば次に進む」

　という通常のスタイルで学習している範囲では

　ほとんどで自覚できなかったこと。

　→筆記具はシャープペンよりエンピツがよい。

　　すべてのメーカーのエンピツを

　　試したわけではないが、

　　試した中ではトンボのMONOや

　　ステッドラーのトラディションが良い感触だった。

　→時間を極限まで短くするチャレンジをすることで

　　限界が近づくにつれ次第に敏感になってきた。

【月別の学習状況　学習日数と学習率】　

　　月　学習日数／日　　　　学習率
----------------------------------------------------
　５月　　１８／１９　　　９４．７％
　６月　　２５／３０　　　８３．３％
　７月　　２２／３１　　　７１．０％
　８月　　２６／３１　　　８３．９％
　９月　　２４／３０　　　８０．０％
１０月　　１０／３１　　　５１．６％　
１１月　　２２／３０　　　７３．３％
１２月　　２７／２８　　　９６．４％
----------------------------------------------------
全体　　１８０／２３０　　７８．２％

【全体をふりかえって】
７月上旬に尿路結石を起こしたときには、

痛みのあまりさすがにプリントを

やろうという気持ちが起きませんでした。

 

たった２～３分の短い時間であっても、

プリントを１枚やるということを

１日の生活に組み込んでおくことで、

結果的にプリントがやれなくても、

プリントをやることに対する

自分の気持ちの向かい具合がどうかがわかるし、

プリントをやってみれば、

その日のアタマの働き具合というか、

自分のコンディションが自分で掴めます。

このことは生活や仕事全般に影響が及ぶもので、

うまく活用すればメリットが

とても大きいように感じました。

また、らくだメソッドを開発した平井氏が

「セルフラーニングは自学自習ではない」

「セルフラーニングはひとりではできない」

「〝自己決定〟とは自分だけで勝手に決めないこと」

　と常々言われているんですが、

　伴走者として見守る指導者の役割は

　とても重要です。

　指導者の立場にあるわたしではありますが、

　こうしてfacebookで学習プロセスを公開し、

　「180枚続ける」ことを宣言してしまうと、

　途中で「や～めた！」とは絶対に言えません。

 

　やらざるを得ない状況に自分を置いてみること、

　つまり、自分の根性や意志、努力に頼るのでなく、

　そのためのしくみづくりの方に意識を向け

　工夫をすることの大事さを改めておもいました。

　つまり、寺子屋塾の教室では

　指導者の私が果たしている伴走者の役割を、

　今回のわたしの学習の場合はfacebookの

　お友達の皆さんが果たして下さったわけで、

　こうして続けられたのは、見守って下さった
　まわりの皆さんのお陰です。（2014.1.3）