事実を柔らかく受け止められる心はどうしたら育つ?(その1)
2023/07/18
昨日投稿した記事に次のように書きました
できない自分を受け入れるというのは、
事実ではなく、
言葉次元の認識にすぎない評価に
自分自身が振り回されず、
重きを置きすぎないということであり、
事実を事実のまま
柔らかく受け止められるような心、姿勢を
自分の中にじっくり腰を据えて
育ててゆくことだとおもうのです。
もちろん、事実を事実のまま
柔らかく受け止めるというのは
言葉で書くほど易しくはない課題であって、
だからこそ、わたしは
それを学習できる場をつくっているわけです。
この記事を読んだ塾生の一人から、
事実を柔らかく受け止められる心は
どうしたら育ちますか?
という質問を受けたので、
それに対する回答を書いてみようとおもいます。
1回の記事だけでは
書き終わらない可能性が高いので、
タイトルに(その1)を付しました。
それで、冒頭の画像に示したように
今日の記事のメインテーマは
「手順を守ってゆっくりやること」について。
らくだメソッドの学習スタイルは、
セルフラーニングと言っているんですが、
「自分で決めて、自分でやる」学習を
すすめていくために、
いくつかの特徴があります。
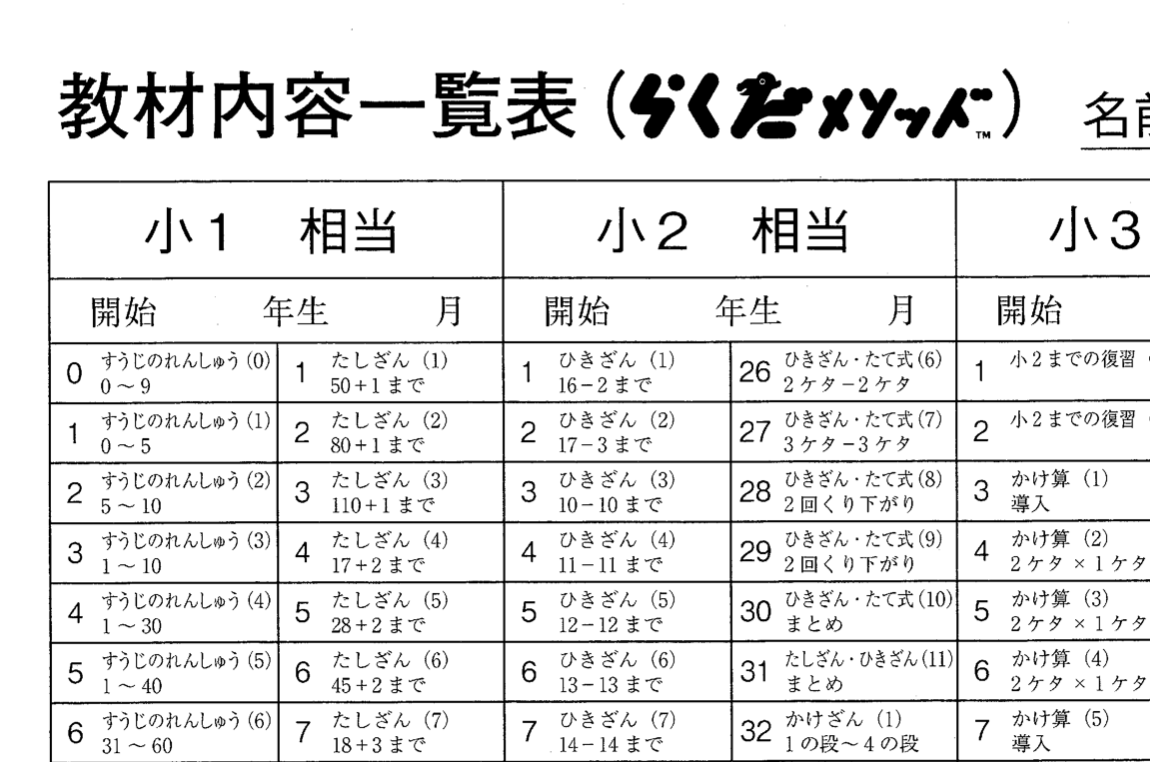
たとえば、上の画像は小学校の算数教材の
教材一覧表の一部分なんですが、
学年相当別に易しい教材から難しい教材へと
スモールステップで
構成されていることもその一つです。
つまり、次のプリントに進んでよいか
それとも同じプリントを繰り返した方がよいか、
学習者が自分で判断するには、
今やったプリントができていたのかどうか、
その基準が明確になっていないといけません。
したがって、らくだメソッドには、
すべてのプリントにめやす時間を設定し、
めやす時間台でできて、
ミスの数が3個以内であれば
合格としているんですが、
たとえば、小学2年生で学習する
かけ算九九の単元であれば、
120題の九九が3分台(3分59秒以内)で
できて、ミスの数が3つ以内であれば、
九九の単元は合格とするわけです。
学校の学習においては、
時間が問題にされることはほとんどありませんが、
ある程度の速さで問題が解けることの
大切さについては、次の記事にあるので、
未読の方は参照ください。
また、らくだメソッドでは
何のためにストップウォッチを使って
時間を計るのかについては
次の記事に書きました。
わたしたちは日常
勉強ができる、勉強ができないという言葉を
よく使いますし、よく聞きます。
わたしも40年近く教育業界という場所で
仕事をしてきたので、
そういう場面に遭遇することが
少なくなかったんですが、
何を根拠にそう言っているのかとなると、
現実にはその基準はとても曖昧で、
明確になっていないことが少なくありません。
それで、第1の重要ポイントとして
結論をまず先に示しておきたいんですが、
それは、基準が明確にあること
(結果がわかること)を
基準にとらわれずにやり続けることなんですね。
つまり、基準のないことをどんなに繰り返しても
自分の正確な実力をつかむことはできないので、
身の程を弁えない妄想が膨らんで、
その妄想にとらわれやすくなりがちです。
でも、だからと言って
その基準を達成することを目指そうとすると、
合格するという目的だけしか
視野に入らなくなってしまいがちで、
自分がどのように問題を解いているのかとか、
どういう癖があるのかなど、
プロセスに対しては意識が向かなくなって
「問題をただ解きさえすればいい」に
なってしまいかねないでしょう。
よって、事実を柔らかく受け止められる心とは、
何かを目指して頑張るような力の入った状態でなく、
なおかつ、力を抜きすぎてもいないような
バランス感の保たれた状態で取り組み、
結果に囚われない大らかな姿勢の持続が
養っていくのではないかと。
まず最初は、問題を解く手順を守って
ゆっくり正確に解くこと・・・と、
言葉で書くとこうなんですが、
結局ここから先は、
個別に体験しながら進めていかないと、
習得することはほんとうに難しいことで、
言葉で伝達することはほぼ不可能な世界なんです。
このことの大事さについて
このblogでは2022年10月に
小4で学習する2けたのわり算を取りあげて
闇雲に数こなせばいいってわけじゃない
というテーマで、6回にわたって
連投記事を書いたことがありました。

たとえば、上の画像は小4−9のプリントで、
1番の問題 100÷32 で、
10÷3つまり100÷30で
仮の商を3と立て、そのままわれるので、
3×2=6,3×3=9 で 96を100から引き
答は、商が3であまり4
2番の問題 120÷32 で、
最初わられる数もわる数も一の位を切り捨て0とし
120÷30を計算して 仮の商4を立てますが、
2×4=8が引けないので4では割れません。
4から1減らして3を立て、
3×2=6,3×3=9 で 96を120から引き
答は、商が3であまり24。
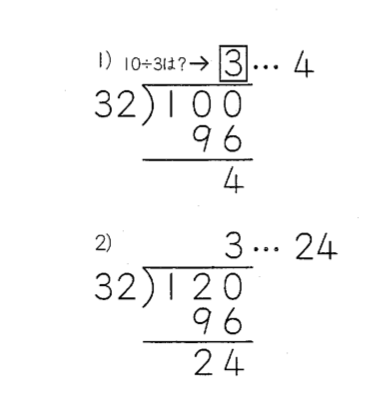
ひとつひとつ手順を守ってていねいに解くので
最初のうちは時間がかかりますが、
だんだんその手順を手が覚えていきますから、
そうした鍛錬を日々積み重ねていくことで、
やがて、問題を見た瞬間に、
正しい商がおもい浮かぶようになってくるのです。
たとえば、これはピアノの練習でも同じです。
最初は楽譜を見ながら、
間違いのないようにゆっくりと練習し、
間違えずに弾けるようになったら、
次に少しずつスピードを上げて弾いてみる・・・
次の動画は、ギリシアの作曲家クセナキスが
1961年に作曲した「ヘルマ」というピアノ作品を
高橋悠治さんが解説しながら弾いているんですが、
5分弱の映像なので視聴してみてください。
Yuji Takahashi_Herma(Iannis Xenakis)
この曲の一番のクライマックスでは、
ピアノの鍵盤88鍵の全音域に
不規則に散らばった30近くの音を
1秒間に演奏しなければならず、
作曲されてから間もない頃には、
高橋悠治さんしか弾けないと言われた超難曲で、
「どうやって練習するんですか?」の問いに
「できる限りゆっくりやって、それから
速くやってみるって、それだけなんだけど」
とぶっきらぼうに答えています。笑

そしてその後に話されていたことが
とても重要だとおもうんですが
「そうすると、手が覚えてくるわけでしょう?
それと、もうひとつは、
暗譜しないとできないんですよ、これは。
少なくともひとつながりの所は覚えていないと、
楽譜を見ながらやってる暇はないんですね」
この続きはまた明日に!
ーーーーーーーーーーーーーーーーーーーーーー
☆寺子屋塾に関連するイベントのご案内☆
◎らくだメソッド無料体験学習(1週間)
詳細についてはこちらの記事をどうぞ!
ーーーーーーーーーーーーーーーーーーーーーー





