もともと知っているのなら、なぜわたしたちは本を読むのですか?
2024/03/02
今日の寺子屋塾blogは、昨日中村教室にいたときに、
塾生から受けた質問に対し
わたしが答えた内容を記録しておこうとおもいます。
|
Q:2/7に投稿されたマイケル・ポランニー『暗黙知の次元 言語から非言語へ』についてのブログ記事を読みました。 数学の問題を解いているとしましょう。
でも、あなたは、その問題の解き方を 先生に教えて貰わなくても、 本来は、もともと知っているし、 その問題を解く能力は もともと備わっているので、 それをおもいだすというか、 素直にそのまま発揮するだけでいいのです。
と書いてあったことに対して、 疑問におもったんです。
もし、もともと知っているってことなら、 なぜ、わたしたちは「本を読む」のでしょう?
本を読むということに、 いったいどんな価値があるのでしょうか?
|
A:今日の名言シリーズに
書いた話なんですが、
栗本慎一郎さんの『パンツをはいたサル』には、
ポランニーが「アインシュタインは、
周りから劣等生と言われていた16歳の頃、
すでに相対性理論の基本的な内容を
確立していた」と発言し、
アインシュタインの存命中に友人を介して
そのことを訊ね、
本人から「確かにそうだ」と返事をもらったという
エピソードが紹介されています。
つまり、新しい科学的発見は、
学校などで積み重ねられた教育の結果として
人間の外部にある客観的な存在から
獲得されるのではなく、もともと
科学者自身の内部に潜んでいる暗黙知の力により
問いが立てられ、解答が与えられるんだと。
その記事にはそのように書いたんですが、
この最後の、
暗黙知の力により問いが立てられ、
解答が与えられる
ってところがポイントなんですね。
アインシュタインは、16歳のときにすでに
相対性理論の基本的なことはわかっていたんだと。
でも、特殊相対性理論の発表は1905年のことで、
彼が26歳のときですから
10年経っていますし、
また、一般相対性理論に至っては
発表されたのは37歳のときですから
20年以上経っていて、
この時間の経過をどう考えるかなんです。
アインシュタイン自身は16歳で
分かっていても、その自分に分かっていることを
アインシュタイン以外の
他の人にもわかるようにするためには、
わかっていることを数式に表したり
言語化したりしなければなりません。
つまり、数学や物理学などの基礎知識はもちろん、
だれもがわかるような
共通理解を得るためには、
言語で記述する表現技術を学ぶ必要があって、
問いが立てられてから
解答が与えられるまでというのは、
アインシュタインにとって、
それだけの年数が
必要だったってことなんですね。

森田真生さんの『数学する身体』のことを
こちらの記事で紹介したことがあったんですが、
そこに書いてあるように、学習ということについて、
ハイデガーはとても興味深いことを言っています。
学ぶってことは、
初めから自分の手元にあるものを
つかみ取ることだ と。
だから、人に何かを教えるってことは、
初めから相手が持っているものを
自分自身でつかみ取るように導くことである と。
でも、教えようとしている相手が
初めから知っていることや
既にわかっていることを教えているのなら、
そこにわざわざ「教える」ってコトバを使うのは
ちょっとヘンなんじゃないかって
おもいませんか?
それでわたしは、
何もそんなふうに遠回しに言わなくても
それは〝教えない教育〟って
言った方がシンプルでいいんじゃないかって
おもっていて、それで寺子屋塾では
この教えない教育を看板にしてるわけなんですが。
でも、多くの人は、学ぶって行為を
自分の外側の世界、つまり外部から知識や情報を
自分の内側に取り込むって感じで
イメージしているんですよね?
だから、公式とかを覚えようとしますよね?
でもね、覚えよう!覚えよう!として
頑張るから、忘れちゃうんですよ。笑
最初から自分の中にあるんだから、
本当は覚えようとしなくていいんですけどね。
たとえば、中3の数学で習う
因数分解なんだけど、
因数分解って、整数あるいは多項式を
整数または単項式と多項式の積、
あるいは、多項式同士の積の形に
変形させるってことだから、
「式の展開」と「因数分解」の関係は、
そのまま「かけ算」と「わり算」の関係と同じ。
つまり、「わり算」(10÷5=2)っていうのは
「かけ算」(2×5=10)の逆演算だから、
「因数分解」は「式の展開」の
逆演算の関係にあたるんだよね。
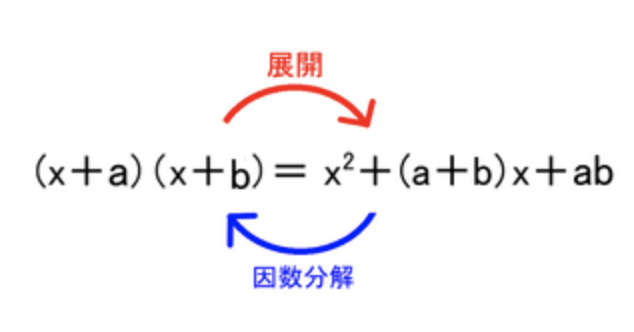
だから、〝因数〟って
日常であまり使わない特殊用語を使うので、
急に難しくなったような感じがしちゃうんだけど、
小学校の算数で習う、
かけ算、わり算の数式が
単に文字式に変わっただけであって、
演算としての本質はまったく変わっていない。
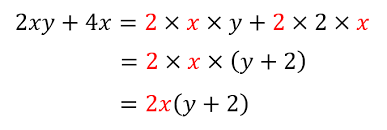
だから、次のような形の
共通因数でくくるっていう因数分解の計算も、
一見複雑で難しそうにみえるけれど、
原理そのものはとてもシンプルで、
式全体を(x+y)でわり算をするってことだから、
かけ算、わり算の数式で表されていることと
ほぼ同義なんだね。

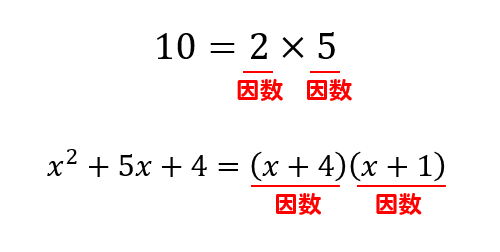
つまり、算数、数学っていう学問は
すべてがこういうふうに積み重なってできていて、
新しい単元が出て来ても、たいていは
前に習ったことや
もともと知っていることを使ってるので、
もともと知っていることと
どのようにつながっているのかを意識して
関連付けながら考えていけばいいんだ。
でも、結構多くの人が
そういう風に考えずに、
外側からやってきた新たな公式を、
アタマで覚えようとしてしまうから、
結果的に覚えられないし、使えないってことに
なりがちなんですね〜。

つまり、自分がもともと知っていることに
結びつけて考えようとしないから、
「自分は〜ができない」「わたしは〜が苦手だ」
というおもいこみの方が勝ってしまい、
誤作動してしまってるわけです。
だから、そうした誤作動というか、
必要のない余計なことをいかに止めるか、
そうした余計なことを
〝考えない〟練習が本来は必要なんだけど。
でも、学校ではそんな風に、
この公式はきみたちが既に
もともと知ってることだよ!
ナンテ教えませんからね。
だから、本を読むということは、
わたしたちがもともと分かっていることを
自分の内側で答え合わせするような感じというか。
つまり、読書するときには、自分の中にある
どういう問いをもとにその本を選んでいるか
意識することが大事であるとか、
書かれていることを覚えようとするんじゃなくて、
自分がすでに知ってたことと
どのように関連付けるかが大事って話を
このブログでも繰り返し書いているわけですし、
自分ではもともとわかっていることなんだけど、
それをまわりの人にもわかるように、
どのように言語化し、どう表現すればいいか、
その表現手段を学ぶってことが
読書の価値じゃないかな。
結局、学習において大事なのは、
「自ら問いを立てる力」であり、
「読み、書き、ソロバン(算数)」ってことに
なるんですね〜
この「読み、書き、ソロバン」の
「読むこと」にスポットを当てた記事を
明日から何回かにわたって書いていく予定です。
※冒頭の画像はアルバート・アインシュタイン
こちらのページより拝借しました
【参考記事】
ーーーーーーーーーーーーーーーーーーーーーーー
●2021.9.1~2023.12.31記事タイトル一覧は
こちらの記事(旧ブログ)からどうぞ
ーーーーーーーーーーーーーーーーーーーーーーー
☆寺子屋塾に関連するイベントのご案内☆
3/10(日) 第25回 経営ゲーム塾Bコース
3/24(日) 未来デザイン考程ワンデイセミナー
4/6(土) 『言葉のズレと共感幻想』読書会#7




