なるべく１度で約分しなさい（その２）

2024/07/26

昨日投稿した記事の続きです。

寺子屋塾生・塩坂太郎くんが

らくだメソッド算数教材で

分数の約分単元を学習していたときに書いていた

ブログ記事を紹介する記事を

旧ブログ〝往来物手習い〟に書いたことがあり、

昨日はその記事をリライトしました。

塩坂くんは、

時間内に「できる」ことを意識しすぎて、
問題の中にある一つの言葉を、素直に
聞いていない

と書いていましたが、

時間内にやり終えることだけを

至上命令として取り組もうとすると、

それ以外の大切なことを無視してしまったり、

見えなくしてしまったりしがちです。

だいいち、そんなやり方は

ミスを生みやすいばかりか

楽しくないですよね〜　疲れますし〜

「手順を守ること」の大切さは

このブログでは繰り返し書いていることですが、

時間を意識すればするほど

遅くなるだけで、

時間が早くなるのは、あくまで結果であり、

時間を意識しないことが、

結果的に早くやれることにつながるので、

最初はとにかく

「ゆっくり」「正確に」解くことなんですね。

２つ以上のことを同時並行的にやる

いわゆるマルチタスクは

非効率的でデメリットが多いことが

最近では心理学や脳科学の研究、実験結果等で

明らかになってきているようで。

ためしに、キーワード「マルチタスク」「効率」で

ググってみてください。

そのような記事がたくさんヒットしますよ〜

つまり、「ミスを減らすこと」と

「時間を短くすること」の両方を

同時並行的に実現しようとするのは

まさにこのマルチタスク的アプローチで、

脳には大きな負担が

かかってるんですね〜。

さて、この分数の約分単元がなぜ重要なのか、

また、この課題に対し、

らくだメソッドでは、

どのような戦略をたてて臨んでいるのでしょうか。

らくだメソッドを開発された

平井雷太さんが著書『らくだ学習法』や

『セルフラーニング　どの子にも学力がつく』

に記されているので、

今日はその文章をご紹介することにしました。

また、記事の終わりに、

過去に寺子屋塾ブログへ投稿した関連記事のうち、

重要なものをピックアップして

まとめておいたので、

未読記事がある方はぜひそちらも確認ください。

（引用ここから）

ーーーーーーーーーーーーーーーーーーーーーー

★約分のポイント——最大公約数を一瞬で見つけるために
らくだメソッドにおいて、きわめて重要な単元の１つが約分です。どうすれば約分ができるのか、そのやり方を知ってはいても、24/36 のような分数の場合、 24/36 = 12/18 = 6/9 = 2/3 というようなやり方で答を求める子どもがいます。このやり方でやっていると、24/36 = 6/9が答であると勝手に判断して、最後まで約分せずに、その途中で計算をやめてしまう場合が多いのです。かと思えば、26/39 や 38/57 のように、分母・分子の公約数に13や19のような大きな素数が入っている場合に、これ以上は約分できないと判断しがちです。

その結果、異分母同士の複雑な分数計算のやり方を知っていても、また途中経過も間違いなくすべてできていても、最後の最後でさらに約分ができることに気がつかなかったばかりに、正解にならなくなってしまうのです。

かといって、次の図のようなやり方で最大公約数を求めるようなことをやっても、もうこれ以上われないというところまでやらずに、途中までの計算（2×2×3 のところを 2×2 でやめてしまう）でそれが最大公約数だと思ってしまう場合もあります。

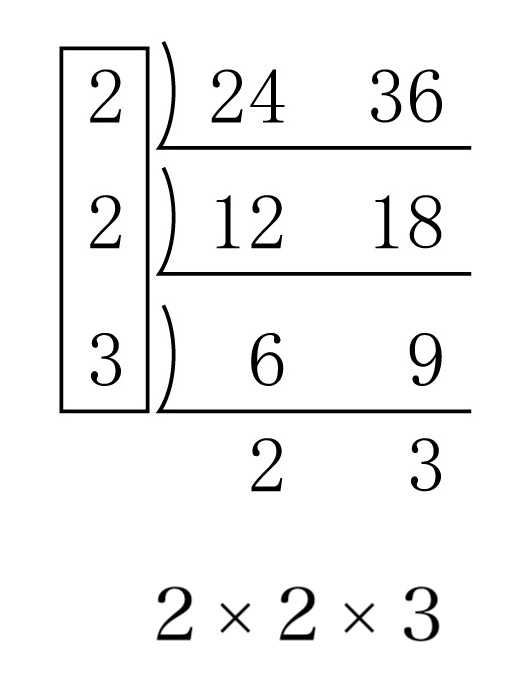
約分教材を作る過程で一番考えたのは、「約分のやり方」を教えることではなく、ある分数を見たときに、「これはもっと約分できる」「これ以上約分できない」という、とっさの判断ができるようにするためにはどうしたらいいのかということでした。

つまり、数感覚の養成です。 26/39 という分数を見たときに、「変だ」「落ち着きが悪い」という感覚を養うためには、まず÷２ケタのわり算がある程度のスピードでスラスラできないと、その感覚も身につかないと判断しました。そのため、約分教材の前には÷２ケタのわり算を１６枚もあてたのです。

たとえば 245 ÷ 45 = のような問題で、どのような数を立てれば答になるかという問題を考えるときに、わる数とわられる数の一の位をかくして、頭の中で瞬時に 24 ÷ 4 = 6、45 × 6 = 270という計算をしているのです。270では245より大きい数になってしまうから、24 ÷ 4 = 6の６を１つ下げて、６→５にして45、45 × 5 = 225。つまり、ここでは÷２ケタの計算をやっていながら、たし算・ひき算・かけ算・わり算を同時に、一瞬のうちにやっているのです。

たし算・かけ算と個別に１つずつスラスラできても、それを同時に処理するようになると、勝手が違ってスラスラはできなくなってしまう。そんな状態のまま、26/39 という分数を見ても、この分数はもっとかんたんになるという判断さえできるわけがないのです。そのため、２けたのわり算の単元では、数感覚を養成するために、64題を１２分台でできることを、１つのめやすとして定めたのでした。

約分教材のプリントではすべてにわたって、99題を７分台でできることを目標にしました。小4-38（次の画像参照）は、約分に入って６枚目のプリントですが、このプリントで求めていることは、一瞬に約分ができること、つまり24/36 = 12/18 = 6/9 = 2/3 の手順を踏んで正解を導くやり方ではなく、24/36 から 2/3 へ一瞬のうちに答を出すことを要求しているのです。

つまり、36と24という２数から、共通の要素（最大公約数）を瞬時に抜き出す能力を育てることを目標にして、教材を作りました。その結果、次のような教材の流れになったのです。

約分の導入プリントでは、2/6 = (　)/3と示して、その下の「分子と分母を2でわって、約分しなさい」との指示を入れました。そして、1番から27番までは、分母分子をすべて２でわるだけで答の出る問題ばかり。28番から54番までは３でわるだけ。55番以降99番までには、２または３でわる問題を混ぜました。

２枚目のプリントでは、1番から27番までは、２または５でわる問題、28番から54番までは３または５でわる問題、そして、55番以降99番までには、２か３か５でわる問題。３枚目のプリントでは、1番から18番までは、２または７で、19番から36番までは３または７で、37番から54番までは５または７で、そして、 55番以降99番までには、2・3・5または７でわる問題を入れたのでした。

４枚目のプリント(小4―36)からは、2・3・5 または７で１回わるだけでは、答にならない問題も混ぜました。その導入は次の画像のような具合です。1番から54番までの問題は、「わけてしても、1度にしてもよい」との指示を出し、55番以降は「なるべく1度で約分しなさい」としました。

５枚目のプリント（小4-37）は、前に図で示した小4-38（６枚目）とまるっきり同じ内容ですが、そこにヒントがついているのです。何でわれば１度で答が出るのかが分かるように、1番の番号の脇に(÷2)、8番の脇には(÷3)。そして、それ以降も÷4、÷5、 ÷6、÷7、÷8、÷9、÷11、÷12、÷13、÷14、÷15、÷16、÷17、 ÷18、÷19、÷20、÷21、÷22、÷24、÷25、÷26、÷28、÷30でできる問題を順に並べて、ヒントをつけたのでした。