なるべく1度で約分しなさい(その5)
2024/07/29
昨日7/28に投稿した記事の続きです。
らくだメソッドの
他の教材にない特徴について、
算数教材の小学4年相当に配当している、
(現行の学習指導要領では小学5年で履修)
分数の約分教材を例にしながら
書いているんですが、
本日分が5回目となりました。
よって、これまでに書いてきた内容を前提として
話を進めることがありますので、
昨日までに投稿してきたの記事のうち、
未読分のある方は、
まずそちらから先にお読み下さい。
これまでの記事をざっとふりかえると、
(その1)は、7年前にわたしが書いたブログ記事で、
分数の約分について触れたことがあり、
その記事はきわめて重要な内容を含んでいるので、
今回リライトして紹介することから始めました。
この連投記事のタイトル
「なるべく一度で約分しなさい」は
その記事のなかで紹介している
塾生の塩坂くんが書いていたブログ記事の
タイトルから拝借したものです。
(その2)は、冒頭でマルチタスク的アプローチの
弊害について紹介し、時間が短縮するのは、
あくまでやり続けた結果として訪れることで、
ゆっくり正確に解く姿勢の大切さを。
また、らくだメソッド開発者・平井雷太さんが
分数の約分単元を攻略するために、
どのような戦略をたてて臨んでいるのか
『セルフラーニング どの子にも学力がつく』に
書かれた文をそのまま引用して紹介し
約分教材全体の構成が垣間見えるようにしました。
(その3)では、教材のスモールステップが
具体的にどんな風に構成されているのか、
小4-33プリントを具体例として紹介しています。
結局、目の前の問題がなぜできないのか、
その原因、理由はひとり一人個別に異なるので、
実際にやってみないと見えてきません。
それで、順序に沿ってやってみることで
個別課題が自ずと浮き彫りになる
構成になっているんですが、
そうなっているからこそ
誰からも急かされることなしに
自分のペースでアプローチできるわけです。
(その4)では、なぜこのメソッドで学ぶと、
自分からすすんでやってみようという
能動的な姿勢が学習者に育ってくるのか、
その秘訣がいったいどこにあるのかについて。
たとえば、約分単元の総まとめとしている
小4-41プリントのように、
300人に1人しか合格できないような
誰もが一朝一夕でできるようにならない
難易度の高い課題を
敢えて設定しているのが何故かを記しました。
さて、それで今日の記事では、
教材の構成について
もう少し詳しく書いてみましょう。
〝教えない教育〟というのは、
別にイジワルで言っているわけではなくて
教えすぎないことによって、
学習者に自問自答の習慣というか、
自分で考える力が身につけられるように
考えてのことでもあります。
とはいえ、教材を順番にやっていくことで、
各々異なる課題が浮き彫りになったときに、
それを学習者本人が
どこまで自覚出来ているかについては、
確認が必要な場合が少なくありません。
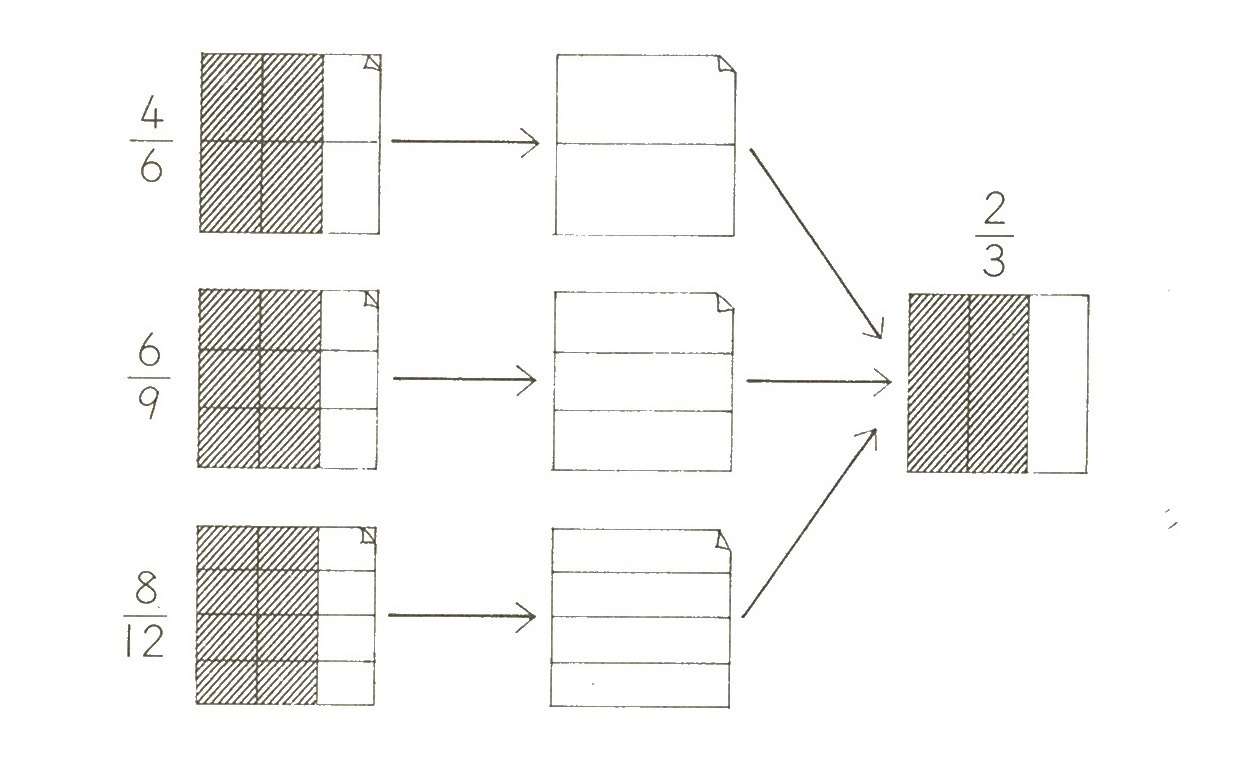
たとえば、学校で使われている
算数の教科書を見ると、
次のような説明が載っています。
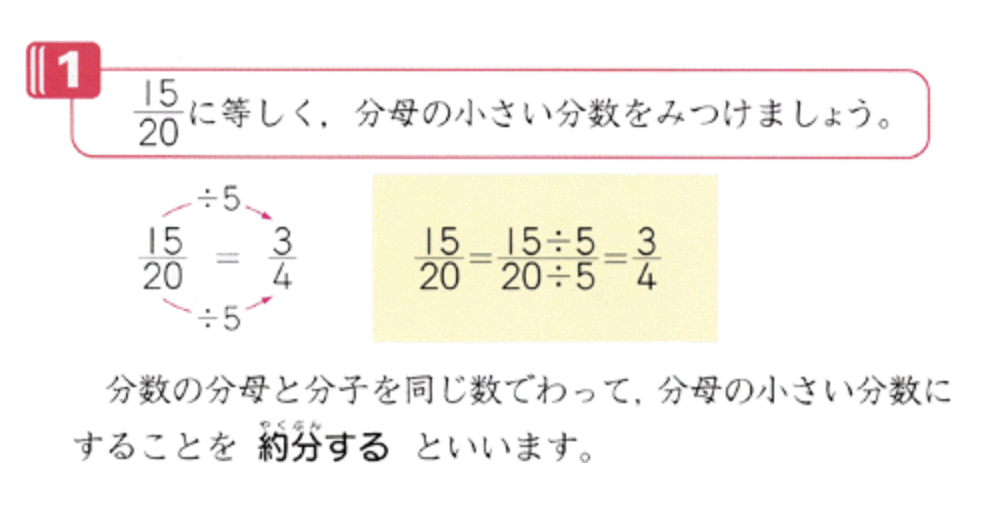
「小学5年」「分数の約分」でググると、
たくさんの記事や動画がヒットしますが、
そのほとんどは、
上の教科書のような発想で、
約分とはどういう概念なのか、
どうやってやればいいのか説明していて
〝教える〟発想なんですね〜
でも、わたしの場合、寺子屋塾を開塾する前に
進学塾に勤めていたときに
徹底的に教える経験をしましたが、
たとえば、約分とはどういうことなのか、
どうやってやればいいのかについて、
懇切丁寧に説明しても、
問題が確実に解けるようにはなっていかない
子どもたちが少なからずいました。
平井さんが書いていたように、
24/36 = 6/9が答であると勝手に判断して、
最後まで約分せずに、
途中で計算をやめてしまったり、
26/39 や 38/57 のように、
分母・分子の公約数に13や19のような
大きな素数が入っている場合には、
これ以上は約分できないと判断してしまうのです。
そうした経験から、
約分の意味や、問題の解き方をわかっていることと
問題が解ける、できるということは、
つながりがまったくないわけではないけれど、
つまり、この2つは
「わかる≠できる」というように、
別次元のことと考えた方がよいのではないかと
考えるようになっていきました。

たとえば、ある事柄が「わかっているかどうか」は
あくまで学習者自身の内的観点でしかないので、
その「わかり方」や
「わかっている度合い」のようなものは
ものすごく個人差があるばかりか、
その「わかり方」「わかっている度合い」を
指導者の立場で確認する術がありません。
しかも、どのような状態になったら
その課題が「できた」ことになるのかという
明確な基準もないので、
約分の概念や問題の解き方が「わかること」と
その問題が「できるようになる」ことを
因果関係で結びつけようとすること自体に
無理があるように感じるのです。

そうです。
泳ぎ方を理解したからといって、
泳げるようになるわけではないように、
わかったからと言って
必ずできるようになるわけではありません。
したがって、指導者の立場でできることは、
自分の説明や話していることを
学習者に分からせよう
理解させようとすることよりも、
マスターすべき課題を細分化して、
易しい課題から難しい課題に順を追って
アプローチできるステップを設けることのほうが
ずっと現実的ではないかと。
そこに、「めやす時間とミスの数3個以内」という
外的観点を導入すれば、
その一つひとつの課題が何ができていて、
何ができないのかが一目瞭然で可視化されるので、
あとは、指導者としては、
その課題の一つひとつを丁寧に確認していけばよく
学習者にとっても
やることがとてもシンプルになるんですね。
これがらくだメソッドの特徴なんですが、
たとえば、(その3)の記事の終わりで紹介した
小4-33のプリントのことで言うと、
※まず、分子と分母を2でわって約分しなさい
※3でわって約分しなさい
※2または3で約分しなさい
と書かれているプリントの指示文を
ちゃんと読まずに無視して、
闇雲に問題をただ解いているだけってことも
少なくありません。
大人の塾生でもそういう人がいるくらいなので、
子どもの場合はなおさらです。
「ここに『2または3で約分しなさい』って
書いてありますが、
このプリントを作った人が
何を言おうとしているかわかりますか?」
「このプリント1枚全部をやることで
達成できる課題はどういうことでしょうか?」
「間違いなく問題が解けるようになることと、
めやす時間内で解けるようになることと
どちらが大切だとおもいますか?」
というように、学習状況に応じた問いかけや
対話的な関わりを丁寧に行っていくことが、
指導者の役割になるわけです。

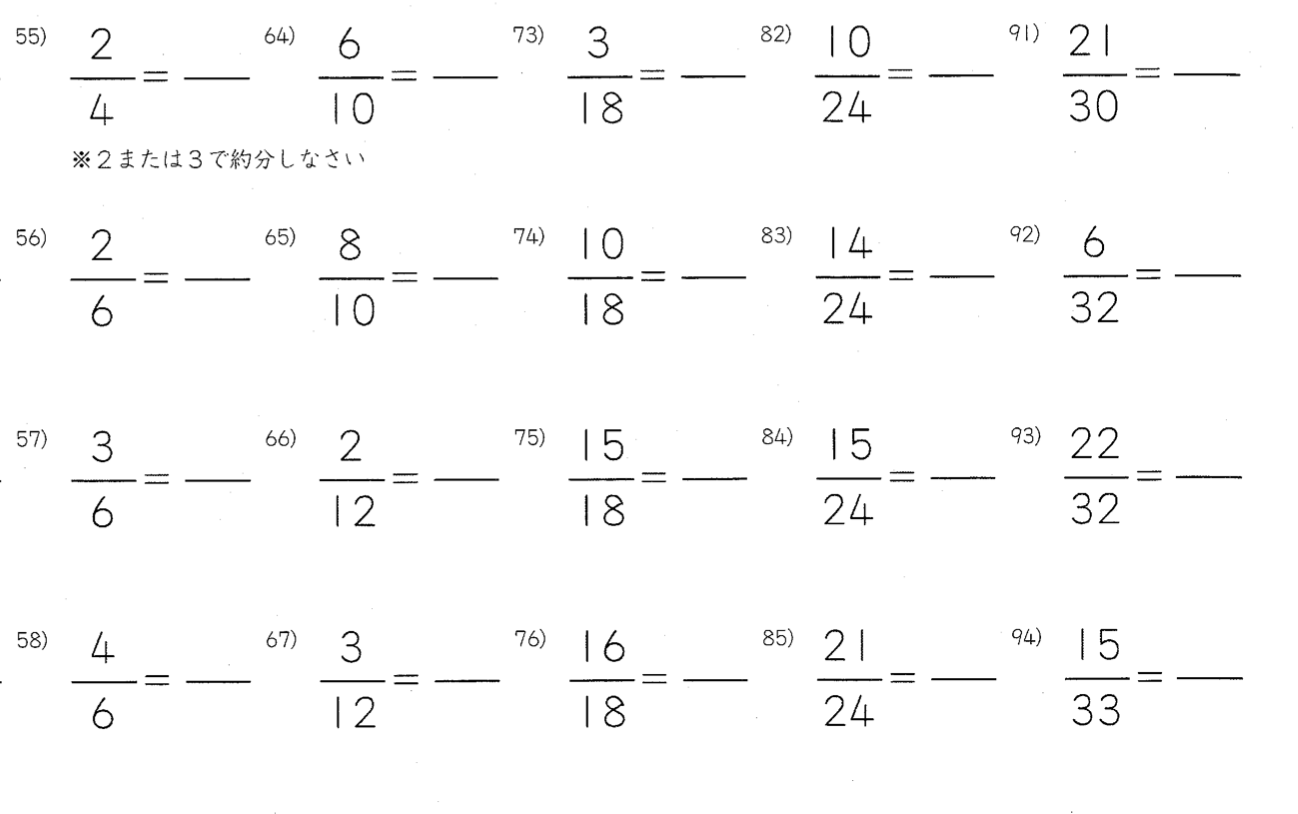
ちなみに、小4-33から35までの
3枚のプリントはすべて、
1回わるだけで既約分数になる問題です。
(既約分数=もうこれ以上約分できない分数)
(その3)の記事で書いたとおり、小4-33は
2か3のどちらで約分できるかが瞬時に判断がついて
自力でスッと答が出せる
習熟度を獲得することが課題です。
よって、54番までの問題をよ〜く観察して、
2でわる分数は、分母も分子もともに偶数
3でわる分数は、分母も分子もともに奇数
分母と分子のいずれかが奇数
になっていると気がつけば、
55番以降の問題も頭を悩ますことなく
スッと約分できるはずなんですね。
そろそろこの連投記事も区切りをつけたいんですが、
この続きはまた明日に!
【過去に投稿した関連記事】
・闇雲に数こなせばいいってわけじゃない!(その1)
・闇雲に数こなせばいいってわけじゃない!(その2)
・闇雲に数こなせばいいってわけじゃない!(その3)
・闇雲に数こなせばいいってわけじゃない!(その4)
・闇雲に数こなせばいいってわけじゃない!(その5)
・闇雲に数こなせばいいってわけじゃない!(その6・最終回)
・事実を柔らかく受け止められる心はどうしたら育つ?(その1)
・事実を柔らかく受け止められる心はどうしたら育つ?(その2)
・事実を柔らかく受け止められる心はどうしたら育つ?(その3)