なるべく1度で約分しなさい(その6・最終回)
2024/07/30
昨日7/29に投稿した記事の続きです。
らくだメソッドの
他の教材にない特徴について、
算数教材の小学4年相当に配当している、
(現行の学習指導要領では小学5年で履修)
分数の約分教材を例にしながら
書いているんですが、
これで6回目になるので
連投記事は本日分にて区切りをつける予定です。
よって、これまでに書いてきた内容を前提として
話を進めることがありますので、
昨日までに投稿してきたの記事のうち、
未読分のある方は、
まずそちらから先にお読み下さい。
さて、昨日投稿した(その5)の記事では、
(その1)から(その4)まで
それまで投稿してきた記事の
概要をふりかえったうえで、
らくだメソッド分数教材の具体的な構成について
さらに詳しく記しました。

この、「わかる≠できる」という言い回しは
らくだメソッド教材の特徴のひとつを
端的に表現していると言ってよいでしょう。
学習者に概念や手順をわからせることによって
できるようにしていこうとするアプローチを
〝教える教育〟とするなら、
できたかどうかを確認することから始め、
概念や手順が後からわかればよいとするアプローチを
〝教えない教育〟となりますが、
らくだメソッドは、
後者の考え方に立ったメソッドだからです。

ただし、これらはあくまで順序の問題ですから、
どちらを選択するかは
教えようとしている中味にもよりますし、
どちらか一方だけが
正しいやり方だと言いたいわけではありません。
でも、算数の計算問題を解くというような
身体の動作を伴う学習に関していえば、
「わかる」「わからない」という
学習者の内的観点に依拠するアプローチよりは、
「ミスの数とめやす時間」というような
外的観点による基準を設けて
一つひとつ確認していくやり方の方が
学習者にとっても指導者にとっても
やることがシンプルになるメリットはあると
わたし自身は感じています。
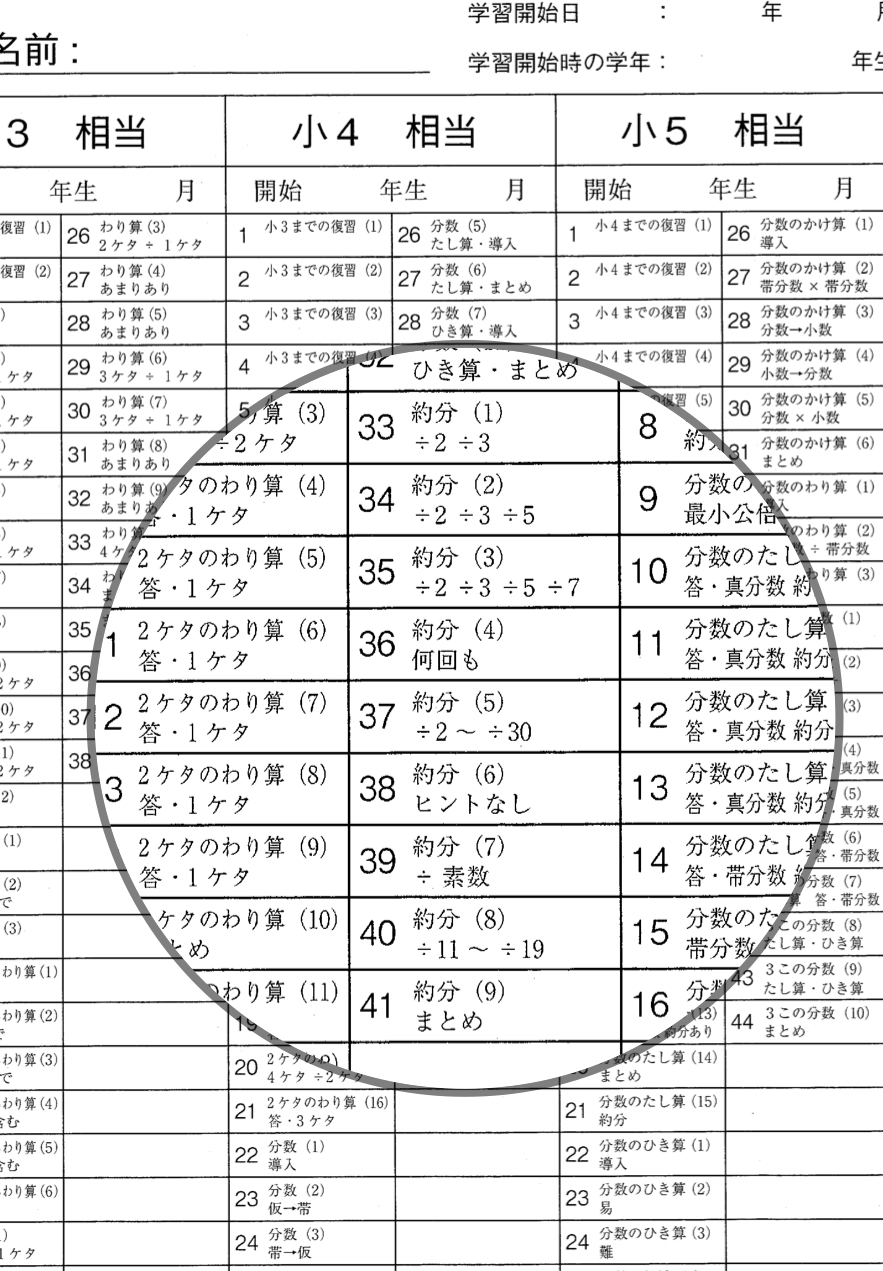
さて前回は、約分単元導入の1枚目にあたる
小4-33のプリントの構成について
具体的に記しましたが、
2でわるのか3でわるのかを
見た瞬間に区別できるようになるのが課題でしたね。

2枚目のプリント小4-34では、
1番から27番までは、2または5でわる問題、
28番から54番までは、3または5でわる問題、
そして、55番以降99番までには、
2か3か5でわる問題になっています。
3枚目のプリントでは、
1番から18番までは、2または7でわる問題、
19番から36番までは、3または7でわる問題、
37番から54番までは、5または7でわる問題、
そして、 55番以降99番までには、
2・3・5または7でわる問題になっています。
つまり、小4-33から35までの
3枚のプリントはすべて、
1回わるだけで既約分数になる問題なんですが、
そのなかでも、
小4-33は、2と3、
小4-34は、2と3と5、
小4-35は、2と3と5と7というように、
番号が1つ進むにつれて、
新しい課題(要素)が1つ加わっていくという
スモールステップの構成でできています。
この難易度設定を適切に行うことが
学習においてはむちゃくちゃ重要なことなので、
繰り返しますが、
2と3が見分けられない段階で、
2と3と5と7を見分けようとしても無理
というか、
脳にものすごく大きな負担を強いることは
わかりますか?
らくだメソッドは、
1枚のプリントに新しい要素1つという原則が
貫かれているのですが、
このことは、手順を踏むことの大切さや
いま、自分がどういう課題に
取り組もうとしているのかを自覚して、
マルチタスクが作動しないように配慮している
点においてもとても重要といえるでしょう。
(その4)の記事の冒頭に入れた
「黄金比と素数」の図については、
その記事中では敢えて説明しなかったのですが、
どうしてこの図があるのか、
約分と素数には密接な関係があるからだと
気づきましたか?
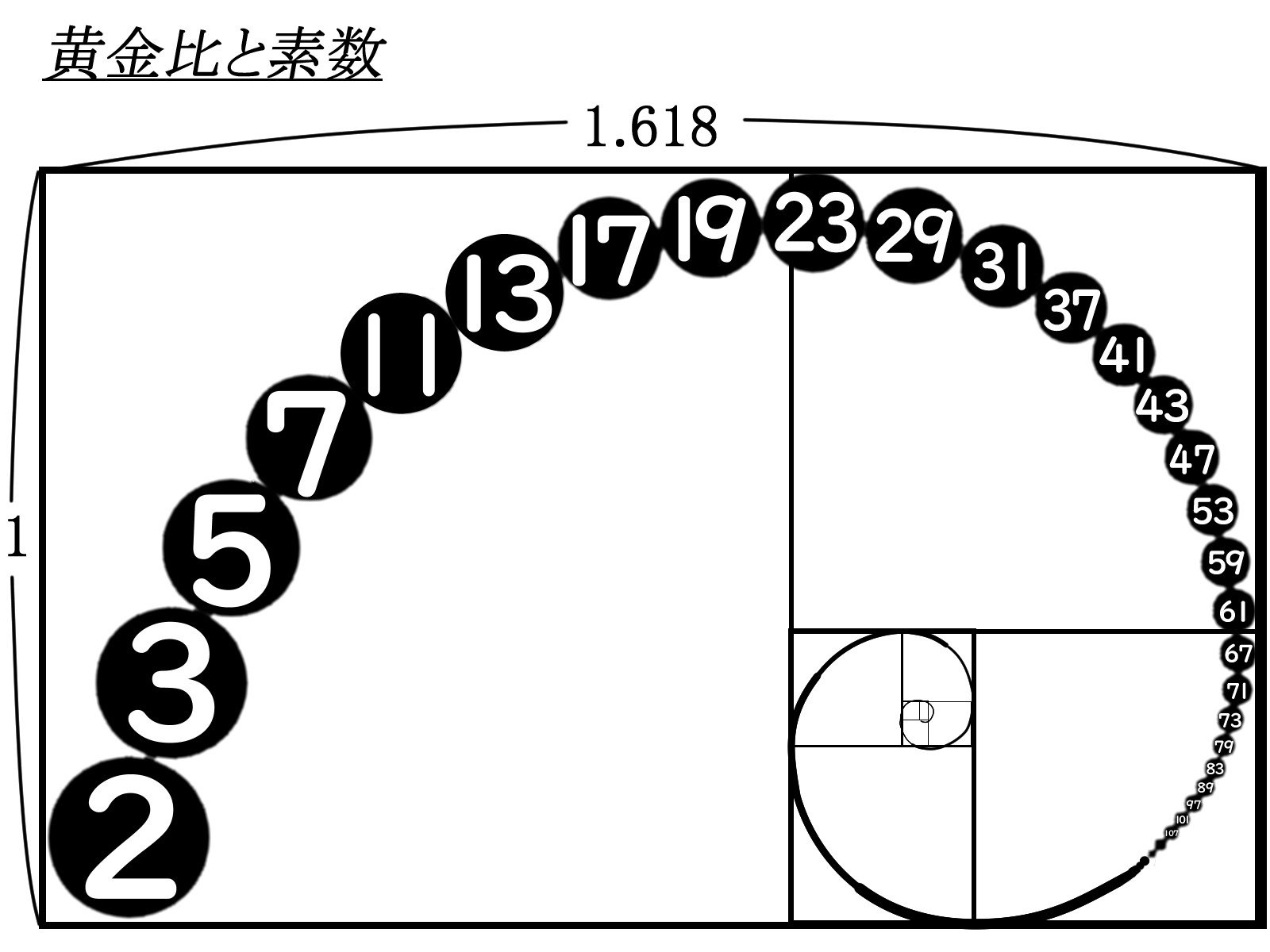
1ケタの素数2・3・5・7でわれば
1回で約分できる分数というのが、
約分問題の中では、
一番易しい問題ということになるので、
小4-33から35までの3枚では、
まず、その範囲で区別できるようになることを
学習課題としているわけです。
さて、それができた上で
4枚目のプリント
小4−36にチャレンジするわけですが、
この小4−36には、
小4-33から35までにはなかった新しい要素、
2・3・5・7で1回わるだけでは
答えにならない約分問題が混ざっていて、
ここでハードルがグンと高くなるんですね。
この「2・3・5・7で1回わるだけでは
答えにならない約分問題」を具体的に書くと、
分母と分子を
4・6・8・9・10・12・14・16・18
という素数ではない数でわって
約分する分数ということになるんですが、
それでも、この小4-36のプリントでは、
1回でいきなり分母と分子の最大公約数でわって
既約分数にすることが
できるようになることを求めていません。
もちろん、小4-33から35までには
なかった数とはいえ
4・6・8・9・10・12・14・16・18
という数は、素因数に分解すると、
4=2×2
6=2×3
8=2×2×2
9=3×3
10=2×5
12=2×2×3
14=2×7
15=3×5
16=2×2×2×2
18=2×3×3
というような具合となります。
つまり、すべて素数2・3・5・7同士の積として
表せるようになるということは、
小4-35までのプリントでやったやり方、
素数2・3・5・7で順番にわっていけば、
約分できるので、
それでもOKとしているわけです。
具体的には、1番から54番までの問題には、冒頭に
「わけてしても、1度にしてもよい」
という指示があり、
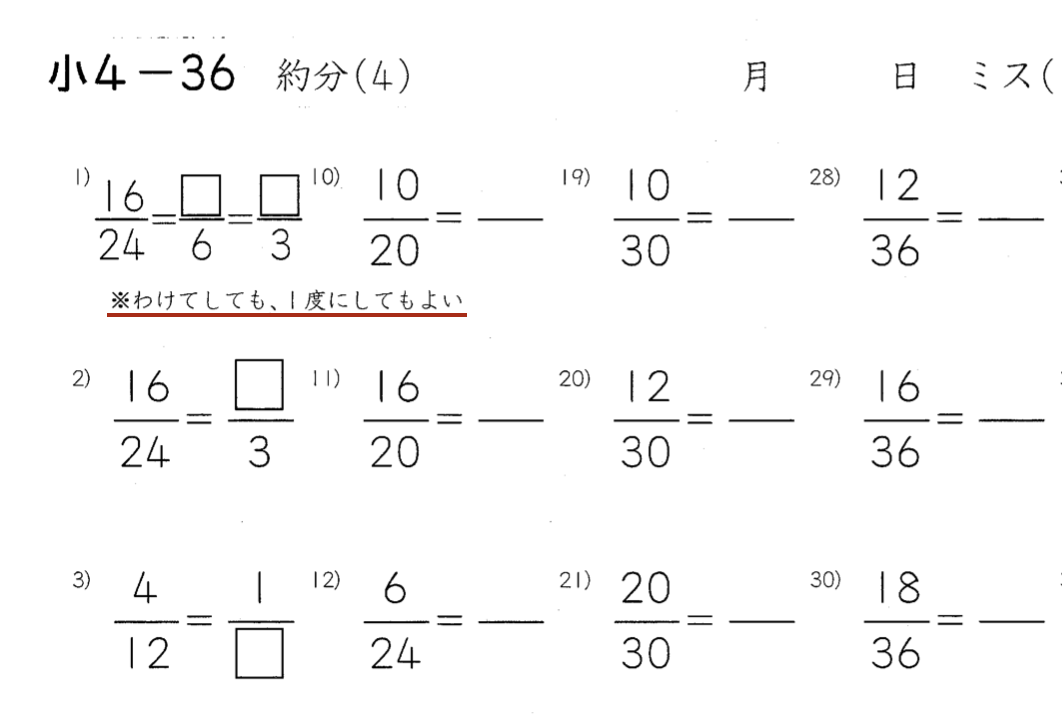
また、55番以降には
「なるべく1度で約分しなさい」という指示が
書かれているんですね。

しかも、55番以降99番までの問題はすべて、
1番から54番までに解いた問題と
同じ問題が再び出てきているだけで
新しい問題は1つもありません。
さて、あなたはこの2つの指示文の
微妙なニュアンスの違いを読み取れますか?
①わけてしても、1度にしてもよい
②なるべく1度で約分しなさい
つまり、①はどちらでもいいという意味ですし、
②は「なるべく」がついているので、
「一度で約分しなさい」と
言っているわけではありませんが、
「一度でしなくていい」とも言っていません。
「一度で約分できなくてもいいけど、
すこしは一度で約分することを
意識しながら問題を解いてね」という含意が
あることが感じられるでしょうか?
②の指示文では、難易度の設定を、
自分の裁量で自由に調節していいと
学習者に任せているわけですが、
言い換えると、
「一度で約分できるようになる」という課題は
とてもハードルが高いので、
その課題をさらに細分化し
「すぐできなくてもいいよ」
「先送りしてもいいよ」と伝えているわけです。
前記したとおり、
1枚のプリントに新しい要素1つという
らくだメソッドの原則がここでも貫かれていて、
小4-36のプリントは、
素数2・3・5・7で2回以上わらないと
既約分数にならない分数が混ざっただけでも、
小4-35と比較すれば
格段にハードルが高くなっているので、
「1度で約分する」という課題は
次の小4-37と小4-38の2枚で取り組むように
設定されているんですね〜

5枚目のプリント小4-37(右側)は、
6枚目のプリント小4-38(左側)と
約分の問題自体はまったく同じ内容です。
でも、小4-37は1番の番号の脇に(÷2)、
8番の脇には(÷3)、
そして、それ以降も÷4、÷5、 ÷6、÷7、÷8、÷9、
÷11、÷12、÷13、÷14、÷15、÷16、÷17、
÷18、÷19、÷20、÷21、÷22、÷24、÷25、
÷26、÷28、÷30というような具合で、
何でわれば1度で答が出るのかが分かるように、
すべての問題にヒントがついていて、
その指示通りにわっていくことが課題で、
小4-38は、ノーヒントで同じ問題に
チャレンジすることが課題になっています。
さてさて、6回にわたり長々と書いてきましたが、
らくだメソッドの算数教材は、
数感覚を養うという意味において、
いわゆる市販されている問題集や計算ドリルとは
全く異なる発想でつくられていることが
多少なりともお伝えできたでしょうか?
そして、こうしたメソッドを活用しながら
寺子屋塾でわたしが日々チャレンジしている
重要な課題のひとつは、
学ぶことを楽しめる人間は
如何にすれば育つかということです。
少し前に論語に載っている孔子の言葉を
紹介した記事を書きました。
・知之者、不如好之者、好之者、不如樂之者(『論語』雍也第六の18 No.137)
その記事にあるとおり、
論語には孔子のこんな言葉が載っています。
物事を知っている者は、
その物事を好んでいる人には及ばない。
物事を好んでいる者は、
その物事を心から楽しんでいる人には及ばない。
つまり、上達したいとおもうのなら、
楽しんでやることが一番の秘訣だね。
もちろん、この学ぶことを楽しむというのは、
一朝一夕で実現できるような
簡単な課題ではありません。
楽しむこと自体が
最終目標になってしまっても困ります。
でも、「できない自分」と出会う学習を
新しい自分に出会うことと認識し、
それが最大の楽しみとおもえるようになったら、
本当に「鬼に金棒」なんだと。
前記した記事の終わりに書いた言葉を
すこし手を加えて
以下に再度記しておきます。
ーーーーーーーーーーーーーーーーーーーーーー
人から強制されて学習しているうちは、
学ぶという行為自体を
なかなか好きにはなれないでしょうし、
まして、そのことを楽しむというのも
難しいのではないでしょうか。
子どもたちが遊んでいるときには、
いま、ここで、ただ遊んでいるだけで、
そこには目的はありません。
子どもは、楽しもうとしているわけではなく、
目的なく、無心に遊んでいるから
結果として楽しいのです。
そういう点から考えると、
自分で決め、自分でやってみる
らくだメソッドにおける
セルフラーニングスタイルの学習は、
何よりもそのことに
楽しみを見い出しやすいし
その人の最高のパフォーマンスを
引き出す可能性を秘めていると言ってよいでしょう。
わたし自身、論語を1日1章ずつ読む試みは、
もともと漢文が苦手科目であったので、
タイヘンに感じたこともありましたが、
読み進めていくうちに
孔子その人が日に日に感じられるようになり、
気がついたときには
できない自分と向き合うプロセスを
楽しみながらやれるようになっていました。
物事を知っている者は、
その物事を好んでいる人には及ばない。
物事を好んでいる者は、
その物事を心から楽しんでいる人には及ばない。
という孔子の言葉は、
2500年という時を経て
今日のようなAIの時代になっても、
AIにはできない、人間だけにしかない
物事を楽しむことの大切さを
語っている点において、
時代を超えた真実であるようにおもうのです。
【過去に投稿した関連記事】
・闇雲に数こなせばいいってわけじゃない!(その1)
・闇雲に数こなせばいいってわけじゃない!(その2)
・闇雲に数こなせばいいってわけじゃない!(その3)
・闇雲に数こなせばいいってわけじゃない!(その4)
・闇雲に数こなせばいいってわけじゃない!(その5)
・闇雲に数こなせばいいってわけじゃない!(その6・最終回)
・事実を柔らかく受け止められる心はどうしたら育つ?(その1)
・事実を柔らかく受け止められる心はどうしたら育つ?(その2)
・事実を柔らかく受け止められる心はどうしたら育つ?(その3)




