雲黒斎『あの世に聞いた、この世の仕組み』(その3)
2024/09/04
昨日投稿した記事の続きです。
雲黒斎さんのこの本の紹介記事は
今日で3回目になるので
これまでの記事が未読の方は次からどうぞ。
昨日引用した箇所の最後は、
Aさんが言う
「ありのままのあなたを受け入れましょう。」と
Bさんが言う
「人間は不完全だから精神修行が大切です。」とは
同じ話をしているって、
いったいどういうことでしょうか?
ってことでした。
今日はまず続き部分を引用してご紹介しますね。
(引用ここから)
ーーーーーーーーーーーーーーーーーーーーーー
「ねぇ雲さん、この矛盾って、どう理解すればいいの?」
実はね、AさんもBさんも、同じ話をしているんだ。一見矛盾しているように見えるけど、 両者がCさんに伝えたがっている内容は同じことなんだよ。
「マジで?」
うん。マジで。
じゃあAさん、Bさんのお話を振り返ってみよう。
自称スピリチュアリストAさんは「あなたは完全・完璧な存在です。ありのままのあなたを受け入れましょう」と言った。
自称宗教家のBさんは「人間は不完全。だからこそ、一人ひとりの精神修行が大切なのです」と言った。
この両者のお話を平面的にとらえると、たしかにまったく逆のことを話しているように思える。おまえの混乱は、まさにこの「平面的な物事のとらえ方」によって生まれたんだ。
本当は同じことを話しているということを理解するためには、物事を平面ではなく立体的にとらえることが必要なんだが……
よし、まずは最初に、この「物事のとらえ方」について説明しよう。
ある日のこと。カツオ君(仮名)とワカメちゃん(仮名)とタラちゃん(仮名)の三人が、人生について語り合っていた。
カツオ君はこう言った。
「人生は、とても素晴らしいものだよ。だって、僕はいつもやさしい人に囲まれ、環境にも恵まれ、体験する出来事にはいつも発見があり、とても楽しい。人生は、僕をやさしく包む愛のようだ。だから、人生を形で表すなら、〝丸〟だね!」
ワカメちゃんはこう言った。
「お兄ちゃん、それは違うわ。人生は、つらく過酷なものだと思う。だって、私はいつも私を攻撃する人に囲まれているし、環境にも恵まれていないし、体験する出来事にはいつも苦渋があって、とても苦しい。人生は、まるで私を突き刺す針のよう。だから、人生を形で表すなら、〝三角〟よ」
タラちゃんはこう言った。
「カツオお兄ちゃんもワカメお姉ちゃんも視野が狭いです〜。 二人とも人生の一部しか見ていないですよ。人生には、楽しいことも、つらいことも、両方あるんです♪だから、人生を形で表すなら、丸い部分も、とがった部分もあるから〝扇形〟です」
さて、この三人の論争の中に、はたして「正解」はあるだろうか?
カツオ君は、「人生は楽しいものだ」と実感しているため、自分の意見が「正しい」と思っている。だから、カツオ君にとっては、ワカメちゃんの意見も、タラちゃんの意見も「間違い」だ。
ワカメちゃんは、「人生はつらく過酷なものだ」と実感しているため、自分の意見が「正しい」と思っている。だから、ワカメちゃんにとっては、カツオ君の意見も、タラちゃんの意見も「間違い」だ。
タラちゃんは、「人生は楽しさと過酷さを併せ持つものだ」と実感しているため、自分の意見が「正しい」と思っている。だから、タラちゃんにとっては、カツオ君の意見も、ワカメちゃんの意見も「間違い」だ。
このままの状態では、これ以上討論を続けても、三人の意見は平行線をたどるだけだよね。
と、そこにサザエさん(仮名)がやってきて、こう言ったんだ。
「三人とも、もっと視野を広げてごらんなさいよ」
そこで「丸」を見ていたカツオ君は、視野を広げるため、一歩下がって遠くから見直してみた。
でも、一歩下がって視野が広がっても「丸」は「丸」のまま。
「三角」を見ていたワカメちゃんが、視野を広げるため、
見直してみた。
一歩下がって遠くから見直してみた。
でも、一歩下がって視野が広がっても「三角」は「三角」のまま。
「扇形」を見ていたタラちゃんが、視野を広げるため、一歩下がって遠くから見直してみた。
でも、一歩下がって視野が広がっても「扇形」は「扇形」のまま。
……う〜ん。困った。視野を広げても、自分の見ていたものが変わらなかったので、三人は、ますます自分の「思い」を「確信」してしまった。
と、今度はそこにマスオさん(仮名)がやってきたんだ。
「どうしたんだい? サザエ」
「あ、あなた、ちょっと聞いて……」
「なるほど。カツオ君たちの意見が食い違っているんだね。じゃあ、こういうのはどうだい?」
そこでマスオさんは三人に『別な角度から見直してごらんよ』とアドバイスしたんだ。
「丸」を見ていたカツオ君がアドバイスを受けて、右斜め45度から見直してみた。
でも、見る角度を変えても「丸」は「楕円」に見えるだけで、「三角」にも、「扇形」にもならない。
「三角」を見ていたワカメちゃんがアドバイスを受けて、右斜め45度から見直してみた。
でも、見る角度を変えても「三角」は「スリムな三角」に見えるだ けで、「丸」にも、「扇形」にもならない。
「扇形」を見ていたタラちゃんがアドバイスを受けて、右斜め45度から見直してみた。
でも、見る角度を変えても「扇形」は「スリムな扇形」に見えるだけで、「丸」にも、「三角」にもならない。
あらら。どうしよう。
三人はますます頑なに「自分の意見に間違いはない」と思ってしまった。
マスオさんもすっかり困り果ててしまったそのとき、玄関先に一人の客人が。
ガラガラガラ......。
「ごめんくださいぃぃぃ〜」
「こ、この声は……アナゴ君っ!ちょうどよかった。 知恵を貸してくれ〜」
「やぁマスオ君。近くに来たんでね、ちょっと寄ってみたんだぁ。あれ?どうしたんです、 みなさんおそろいでぇ。え? カツオ君たちがぁ……ふむふむ、なるほどぉ」
そんなこんなで、今度はアナゴさんがアドバイスすることになったんだ。
「いいかい、君たちはぁ、物事を〝平面的〟にとらえているんだぁ。自分の主観以外の可能性を認めず、自分の考えに執着してしまうからぁ、意見が食い違ってしまうんだよ。物事はぁ〝立体的〟に考えたほうがいい〜」
「立体的に考える?」
「うん。カツオ君もぉ、ワカメちゃんもぉ、タラちゃんもぉ、三人とも形を〝丸・三角・扇形という二次元〟でとらえていたんだぁ。だからほらぁ、お互いの意見を頭から否定せず、尊重しあって次元を上げてごらん」
※雲黒斎『あの世に聞いたこの世の仕組み』第10章「自我と真我」より
ーーーーーーーーーーーーーーーーーーーーーー
(引用ここまで)
最後のアナゴさんの言葉
〝立体的〟に考えたほうがいい〜
お互いの意見を尊重しあって次元を上げるって、
具体的にどういうことを言おうとされているか
雲黒斎さんの文章を読まれて
わかりましたか?
Aさんが言われた
「ありのままのあなたを受け入れましょう。」と
Bさんが言われた
「人間は不完全だから精神修行が大切です。」を
立体的に捉えるとどうなるかを
ぜひ、ご自身で考えてみてください。
学習のふりかえり文を紹介した記事の中に、
次のような文章を書いたコトがあります。
……毎日の気づきを
「点としての気づき」と呼ぶなら、
2ヶ月分の「点としての気づき」を
読みなおして書かれたこのようなふりかえり文は
「線としての気づき」と言ってよいでしょう。
ちょうど今回は学習開始後半年を迎えられたので、
2ヶ月毎に書かれている「線としての気づき」自体を
通してふりかえって
半年間をふりかえった「面としての気づき」文も
含まれた内容になっていましたね。
つまり、「点としての気づき」
「線としての気づき」
「面としての気づき」
は同じふりかえり文であっても次元が異なるわけです。
このようにインターバルを変えてふりかえることを
繰り返し実践されることを続けられることは、
自分を多次元多面的に捉えることにつながり、
学習自体を自己管理することが
可能になっていくわけです……
前後の文脈があるので、未読の方は
この引用した箇所だけでなく、
ぜひモトの記事の方を読んで戴きたいんですが。
先月書いた内的観点と外的観点、の記事の最終回で、
「統合」というキーワードを提示したんですが、
覚えていますか?
たとえば、地球外に出る経験をした宇宙飛行士から
宗教家になる人が輩出するということは、
その人が地球外に出ることで、
いったい何を獲得したのかというと、
ただ、視野を広くしただけではなく、
ただ、見る角度を変えただけではなく、
自分の外界を捉える認識の次元が上がって
統合されたってことなんですね。

つまり、それまでAとBしか見えなかったのに、
AとBが〝統合〟されることによって、
認識の解像度が上がり、
それまでの自分には見えていなかった
Cが見えてきたんだと。
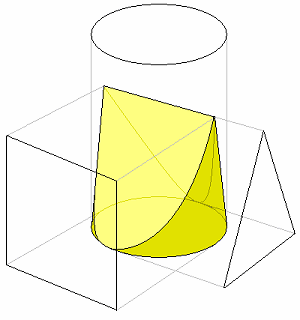
また、次の図の3つの図形は、
平面的に捉えれば、
丸と三角と四角にしか見えないですよね?

でも、これらの二次元で書かれた
3つの図形を統合し、
三次元の立体として捉えられると、
次のようないわゆる3D画像になるわけです。
この続きは明日投稿予定の記事で!




