陰と陽とは何か⑰「練習問題集〝クラックス〟（その２）」

3-17 実体のない「心」が物理的な「六角形」をしている
ちょっと待てよ、と思うよね？「心」は実体のないものだ。つかみどころがない。「これだ」と指すことはできない対象だ。でも、その実体のない心が、物理的な「六角形」をしているとは一体なにごとだ、という話になってくる。精神と物質が混在していて、議論がフワフワとしている。

僕は、こんなふうに焦点が定まらず、哲学的な気分になると、いつも、あの南米ボリビアのウユニ塩原が脳裏に浮かんでくる。風景が水面に全反射して、足元が空になる。上を向いても空。下を向いても空。宙に浮かんで青空を漂っている気分。

自分が見ているものは一体なんだろう。自分の感じているものは一体なんだろう。脳は一体なにをしているのだろう―。そんな浮遊感を旅するとき、あの大好きなウユニ塩原の風景が思い出される。

ウユニ塩原は雨期になると、あんなふうに薄く水が張って、風景が水面に全反射する。ウユニ塩原の標高は3700メートルだ。富士山の標高は。

——3776メートル。

富士山と同じくらいの高地に、あの幻想的な風景がある。おもしろいことに、乾期になると、すっかり水が干上がってしまう。そう。その乾いた大地の風景を見てほしい。

これが乾期のウユニ塩原の写真だ。ほら、なにか気になるものが見えるね。

——うわ、六角形！

干からびて、地面にバキバキとヒビが入ると、六角形に割れる。なんじゃこりゃ、だね。でも、ウユニ塩原に限らない。六角形は、実は、自然界にたくさんある。たとえば、イギリスの北アイルランドのジャイアンツ・コーズウェイ。

とても有名な岩場で、ユネスコの世界遺産に登録されている。この岩場も、よく見ると、六角形に割れている。六角柱だね。こうした柱状節理は、日本でも、福井県の東尋坊をはじめ、各地で見られる。そんなふうに六角形は、自然界ではまったく例外ではない。普通に存在する。君らが思いつく六角形は何かな？

——ハチの巣。
——雪の結晶。

そうだね、ハチの巣も雪の結晶も六角形だ。ほかに?

——ベンゼン環とか。

ベンゼン環。おお、たしかに六角形だ。これは思いつかなかった。ところで、ベンゼン環のことを世間の一般の人々は、何と呼ぶ？とくに、化学が苦手な人がベンゼン環を揶揄するように示す言葉。

——亀の甲羅。
——あ、亀も六角形だ。

そうだね。ほかにはツクシの頭も、六角形だよね。虫めがねでツクシの先端を見たことはある？　あとは、トンボの目も拡大すると六角形だ。キリンの模様もそうだね。六角形はそこここにある。四角形はあまりないけれど、六角形はあたりまえの存在だ。

3−18 とにかく六角形になってしまう

ここで、君らに、また実験してほしい。六角形は簡単に現れることを体験してもらいたいんだ。紙粘土を用意した。色とりどりの紙粘土だ。紙粘土を丸めてボール状にする。同じ大きさのボールを、テーブルの上にぎっしりと並べて、上から圧力をかけてつぶす。すると、丸いボールが六角形になる。角のない球形から六角形が生まれるなんて信じられないかな。やってみよう。粘土を丸めて、並べてね。

——……(黙々と作業)。

できた。綺麗に並べてもらったね。そうしたら、次に、この平らな板を使って、並べた粘土ボールを一気に押しつぶす。

——僕らからやります。

よし。押してみて。軽く力を入れるだけでいいよ。はい、おお、いいね。そうしたら、板を取り除いてみてごらん。

——（一同）おお！

結果を知っていても、実際にやってみると、感動するよね。もう、わかったね。自然界で規則正しい六角形の配列ができることは、摩訶不思議な現象ではない。たいして複雑な原理もないまま、小細工なしに、とにかく六角形になってしまう。四角形より六角形のほうが自然なんだ。グリッド細胞の話に戻れば、グリッド細胞が120度の座標系になっているのも、僕らの心が六角形になっていることも、さして驚くことはない。むしろ、六角形が自然。自然からしてみれば、そりゃそうだよ、といった具合なんだ。

実際、六角形が自然に現れることは、数学的にも妥当な現象だ。妥当だし、合理的。たとえば、ハチの巣はなんで六角形なんだろう?

——壊れにくい。

そのとおり。この構造は強い。外圧に対して頑強で、つぶれにくい。利点はほかにもある。たとえば、同じ容積のなかに、もっともたくさんハチの子を入れられる。つまり、限られた空間をもっとも効率よく活用できる。それが六角形の部屋の配置だ。しかも少ない材料でたくさん収納できる。巣の壁をつくる材料は、できれば節約したい。できる限り少ない材料で、できるだけたくさん部屋を確保しようとすると、あの六角形がもっとも効率的。つまり、六角形は空間資源という意味でも、物質資源という意味でも、省エネなんだ。ハチの巣はあんなに軽いのに頑丈だ。だから、ロケットのフェアリングにも、この六角形のアイデアが応用されている。機体を軽くするためにね。

グリッド細胞の話に戻そう。嗅内野に電極を刺して、動物を走らせてどこで神経細胞が発火するかを見ると、六角形の格子状になっている、という発見だったね。グリッド細胞の発見は、場所細胞の発見と同時に、ノーベル生理学・医学賞が与えられた大発見だ。グリッド細胞は嗅内野に存在する。そこで、嗅内野のどこにグリッド細胞が存在するかを、顕微鏡で調べたマップがこれ。

——わお……。

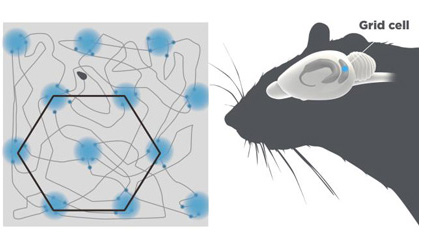
おもしろいよね。グリッド細胞は、グリッド状に発火するだけでなく、その細胞が存在する配置の具合も、なんと、グリッド状。六角形にばらまかれていたんだ。嗅内野にまんべんなく存在しているのではなくて、グリッド細胞の配置そのものがグリッド状になっていた。神経反応も、神経配列も、ともに六角格子状なんだ。もう「ほんと六角形が好きだねえ……」と呆れるくらい、自然界は六角形に満ちている。先ほど紙粘土で実験してもらったように、六角形はおそろしく簡単に発生する。だから、生物が六角形を積極的に好んで採用しているのか、あるいは、自然に逆らったとしても、どうしても六角形になってしまうのか、そこまではわからないけど、ともかく六角形なんだ。つまりね、自然は壮大で変幻自在だからといって、何だってできるわけではない。自然は自由ではない。ある制約のもとに自然界は存在している。その制約の一つが、ずばり、六角形だ。